函数的性质通常指函数的定义域、值域、奇偶性、周期性、单调性等,请选择适当的探究顺序,研究函数 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在 上的图象.
上的图象.
(本小题满分12分)已知 .
.
(1)若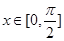 且
且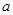 =l时,求
=l时,求 的最大值和最小值,以及取得最大值和最小值时x的值;
的最大值和最小值,以及取得最大值和最小值时x的值;
(2)若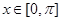 且
且 时,方程
时,方程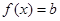 有两个不相等的实数根
有两个不相等的实数根 ,求b的取值范围及
,求b的取值范围及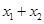 的值.
的值.
(本小题满分12分).已知函数 .
.
(Ⅰ)求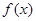 的周期和振幅;
的周期和振幅;
(Ⅱ)在给出的方格纸上用五点作图法作出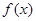 在一个周期内的图象.
在一个周期内的图象.
(Ⅲ)写出函数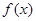 的递增区间.
的递增区间.
(本小题满分10分)已知函数 的最小正周期为
的最小正周期为 ,
,
(1)求函数 的表达式并求
的表达式并求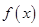 在区间
在区间 上的最小值;
上的最小值;
(2)在 中,
中,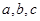 分别为角
分别为角 所对的边,且
所对的边,且 ,
, ,求角
,求角 的大小;
的大小;
(本小题满分10分)已知向量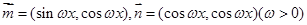 ,设函数
,设函数 ,且
,且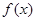 的最小正周期为
的最小正周期为 .
.
(1)求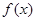 的单调递增区间;
的单调递增区间;
(2)先将函数 的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,然后将图象向下平移
的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,然后将图象向下平移 个单位,得到函数
个单位,得到函数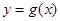 的图象,求函数
的图象,求函数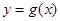 在区间上
在区间上 上的取值范围.
上的取值范围.