(本小题满分12分)在直角坐标平面内,已知点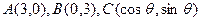 ,其中
,其中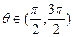 .
.
(Ⅰ)若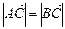 ,求角
,求角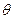 的弧度数;
的弧度数;
(Ⅱ)若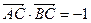 ,求
,求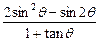 的值.
的值.
已知 ,
, ,且
,且
(1)求函数
 的单调增区间;
的单调增区间;
(2)证明无论 为何值,直线
为何值,直线 与函数
与函数 的图象不相切.
的图象不相切.
(本小题满分13分)已知向量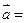
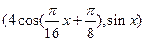 ,
,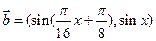 ,
,
定义函数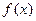 =
=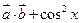 。
。
(Ⅰ)求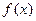 的最小正周期;在所给的坐标系中作出函数
的最小正周期;在所给的坐标系中作出函数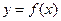 ,
,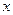 ∈
∈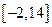 的图象
的图象
(不要求写出作图过程);
(Ⅱ)若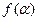 =2,且14≤
=2,且14≤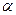 ≤18,求
≤18,求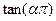 的值
的值
已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)若 在
在 处取得最大值,求
处取得最大值,求 的值;
的值;
(Ⅲ)求 的单调递增区间.
的单调递增区间.
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
 |
0 |
 |
 |
 |
 |
 |
0 |
1 |
 |
0 |
 |
0 |
(1)求 的解析式;
的解析式;
(2)若在 中,
中, ,求
,求 的值.
的值.
若 ,其中
,其中 ,记函数
,记函数
(1)若 的图像中两条相邻对称轴间的距离
的图像中两条相邻对称轴间的距离 ,求
,求 及
及 的单调减区间。
的单调减区间。
(2)在(1)的条件下,且 ,求最大值。
,求最大值。
若 (
( ,
, ,已知点
,已知点 ,
, 是函数
是函数 图象上的任意两点,若
图象上的任意两点,若 时,
时, 的最小值为
的最小值为 ,且函数
,且函数 为奇函数.
为奇函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数 的图象,求函数
的图象,求函数 的单调递增区间.
的单调递增区间.
已知向量 ,设函数
,设函数 。
。
(1)求函数  的最小正周期及
的最小正周期及 时的最大值;
时的最大值;
(2)把函数 的图象向左平移
的图象向左平移
 个单位,所得到的图象对应的函数为奇函数,求
个单位,所得到的图象对应的函数为奇函数,求 的最小值。
的最小值。