湖北省八市高三年级第一次联考数学(理)试题
设全集为 ,用集合
,用集合 的交集、并集、补
的交集、并集、补 集分别表示右边韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为:Ⅰ部分:
集分别表示右边韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为:Ⅰ部分: ,Ⅱ部分:
,Ⅱ部分: ,Ⅲ部分:
,Ⅲ部分: ,Ⅳ部分:
,Ⅳ部分: ,其中表
,其中表 示错误的是 ( )
示错误的是 ( )
| A.Ⅰ部分 | B.Ⅱ部分 | C.Ⅲ部分 | D.Ⅳ部分 |
函数 的最小正周期为
的最小正周期为 ,则该函数的图像( )
,则该函数的图像( )
A.关于点 对称 对称 |
B.关于直线 对称 对称 |
C.关于点 对称 对称 |
D.关于直线 对称 对称 |
设抛物线 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ,以
,以 ,
, 为焦点,离心率为
为焦点,离心率为 的椭圆的两条准线之间的距离为 ( )
的椭圆的两条准线之间的距离为 ( )
| A.4 | B.6 | C.8 | D.10 |
3个要好的同学同时考上了同一所高中,假设这所学校的高一年级共有10个班,那么至少有2人分在同一班级的概率为 ( )
A. |
B. |
C. |
D. |
假设某市今年高考考生成绩 服从正态分布
服从正态分布 ,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中
,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中 )
)
(本小题满分12分)甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为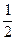 ,乙投篮命中的概率为
,乙投篮命中的概率为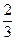 .
.
(Ⅰ)求甲至多命中2个且乙至少命中 2个的概率;
2个的概率;
(Ⅱ)若规定每投蓝一次命中得3分,未命中得-1分,求乙所得分数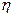 的概率分布和数学期望.
的概率分布和数学期望.
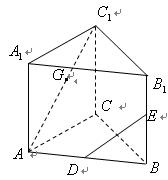
(本小题满分12分)如图,在正三棱柱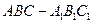 中,
中,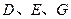 分别是
分别是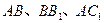 的中点,
的中点,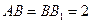 .
.
(Ⅰ)在棱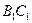 上是否存在点
上是否存在点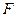 使
使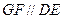 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面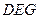 与底面
与底面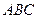 所成锐二面角的正切值;
所成锐二面角的正切值;
(Ⅲ)求点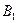 到截面
到截面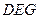 的距离.
的距离.
(本小题满分12分)如图,用一块形状为半椭圆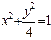
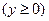 的铁皮截取一个以短轴
的铁皮截取一个以短轴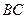 为底的等腰梯形
为底的等腰梯形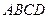 ,问:怎样截才能使所得等腰梯形
,问:怎样截才能使所得等腰梯形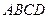 的面积最大?
的面积最大?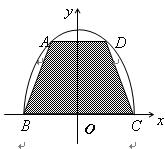
(本小题满分13分)已知两定点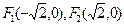 ,平面上动点
,平面上动点 满足
满足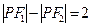 .
.
(Ⅰ)求动点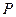 的轨迹
的轨迹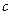 的方程;
的方程;
(Ⅱ)过点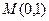 的直线
的直线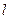 与
与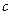 交于
交于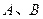 两点,且
两点,且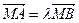 ,当
,当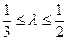 时,求直线
时,求直线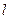 的斜率
的斜率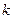 的取值范围.
的取值范围.
 表示平面,
表示平面, 为直线,下列命题中为真命题的是 ( )
为直线,下列命题中为真命题的是 ( )



 为等比数列,
为等比数列, ,且
,且 ,则
,则




 ,若
,若 ,则
,则 的取值范围是 ( )
的取值范围是 ( )



 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值
的最大值 与最小值
与最小值 的比
的比 =" " ( )
=" " ( )



 是
是 的展开式中
的展开式中 的一次项的系数,则
的一次项的系数,则
 (
( 为自然对数的底数)的实根个数为 ( )
为自然对数的底数)的实根个数为 ( ) 是虚数单位,
是虚数单位, ,若
,若 ,则
,则 .
. 是直线
是直线 上不同的三个点,点
上不同的三个点,点 不在直线
不在直线
 为实
为实 数,则使
数,则使 成立的充分必要条件是 .
成立的充分必要条件是 .
 中,
中, ,则
,则 两点间的球面距离为 .
两点间的球面距离为 . 满足下列关系:
满足下列关系:
 (
( 为非零常数)
为非零常数)

 的解析式为
的解析式为 .
.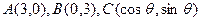 ,其中
,其中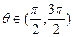 .
.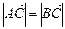 ,求角
,求角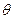 的弧度数;
的弧度数;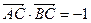 ,求
,求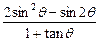 的值.
的值. 行的第一个数为
行的第一个数为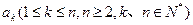 .
.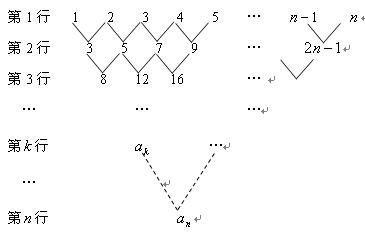
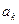 与
与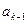 的递推关系,并求
的递推关系,并求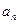 ;
;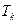 ;
;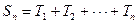 ;并证明:当
;并证明:当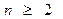 时,
时,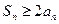 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号