已知向量 ,
, ,
, ,其中
,其中 为
为 的内角.
的内角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,求
,求 的长.
的长.
函数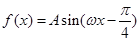 (
(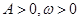 )的部分图像如右所示.
)的部分图像如右所示.
(1)求函数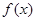 的解析式;
的解析式;
(2)设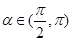 ,且
,且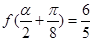 ,求
,求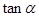 的值.
的值.
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设 ,
, ,
, ,求
,求 的值.
的值.
设函数f(x)=  ×
× ,其中向量
,其中向量 ="(2cosx,1),"
="(2cosx,1),"  =(cosx,
=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0, ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
已知函数
,其中常数
(1)令
,判断函数
的奇偶性,并说明理由;
(2)令
,将函数
的图象向左平移个
单位,再向上平移1个单位,得到函数
的图象,对任意
,求
在区间
上零点个数的所有可能值.
已知函数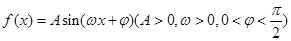 部分图象如图所示。
部分图象如图所示。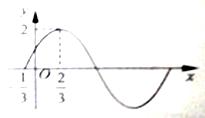
(1)求函数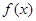 的解析式;
的解析式;
(2)当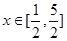 时,求函数
时,求函数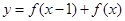 的值域。
的值域。
已知函数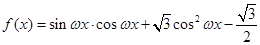
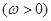 ,直线
,直线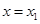 ,
, 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且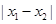 的最小值为
的最小值为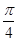 .
.
(1)求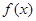 的表达式;
的表达式;
(2)将函数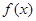 的图象向右平移
的图象向右平移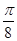 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐
标不变,得到函数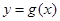 的图象,若关于
的图象,若关于 的方程
的方程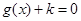 ,在区间
,在区间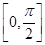 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数 的取值范围.
的取值范围.
【原创】(本小题满分12分)已知函数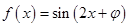 (
(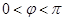 )的图象过点
)的图象过点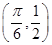 .
.
(1)求函数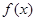 的解析式;
的解析式;
(2)若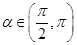 ,
, ,求
,求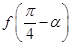 的值.
的值.
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(2)当 时,求函数
时,求函数 的取值范围.
的取值范围.