[广东]2013届广东省韶关市高三第一次调研测试数学理科试卷
某几何体的三视图如图所示(俯视图是正方形,正视图和左视图是正三角形),根据图中标出的数据,可得这个几何体的表面积为( )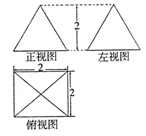
A.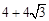 |
B.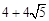 |
C.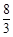 |
D.12 |
在实验员进行的一项实验中,先后要实施5个程序,其中程序A只能出现在第一步或最后一步,程序C和D实施时必须相邻,请问实验顺序的编排方法共有
| A.15种 | B.18种 | C.24种 | D.44种 |
设 在区间
在区间 上有定义, 若
上有定义, 若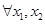
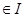 , 都有
, 都有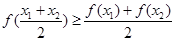 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若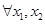
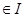 , 都有
, 都有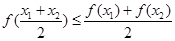 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则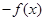 是区间
是区间 的向下凸函数;
的向下凸函数;
②若 和
和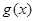 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则 是区间
是区间 的向上凸函数;
的向上凸函数;
③若 在区间
在区间 的向下凸函数且
的向下凸函数且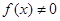 ,则
,则 是区间
是区间 的向上凸函数;
的向上凸函数;
④若 是区间
是区间 的向上凸函数,
的向上凸函数, , 则有
, 则有

其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
平面上有 条直线, 这
条直线, 这 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这 条直线将平面分成
条直线将平面分成 部分, 则
部分, 则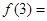 ___________,
___________,  时,
时, _________________.)(用
_________________.)(用 表示).
表示).
(几何证明选讲选做题)如图,AB、CD是圆的两条弦,
且AB是线段CD的中垂线,已知AB=6,CD=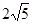 ,则线段AC的长度为 .
,则线段AC的长度为 .
(坐标系与参数方程选做题)在直角坐标系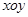 中,圆
中,圆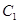 的参数方程为
的参数方程为 (
(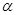 为参数)在极坐标系(与直角坐标系
为参数)在极坐标系(与直角坐标系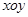 取相同的长度单位,且以原点
取相同的长度单位,且以原点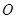 为极点,以
为极点,以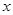 轴的正半轴为极轴)中,圆
轴的正半轴为极轴)中,圆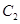 的极坐方程为
的极坐方程为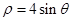 ,则
,则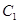 与
与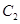 的位置关系是______(在“相交、相离、内切、外切、内含”中选择一个你认为正确的填上).
的位置关系是______(在“相交、相离、内切、外切、内含”中选择一个你认为正确的填上).
某校为了解高二学生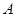 、
、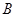 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试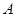 、
、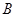 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2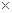 2列联表:
2列联表:
| |
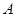 学科合格人数 学科合格人数 |
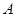 学科不合格人数 学科不合格人数 |
合计 |
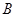 学科合格人数 学科合格人数 |
40 |
20 |
60 |
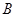 学科不合格人数 学科不合格人数 |
20 |
30 |
50 |
| 合计 |
60 |
50 |
110 |
(1)据此表格资料,你认为有多大把握认为“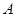 学科合格”与“
学科合格”与“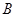 学科合格”有关;
学科合格”有关;
(2)从“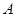 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“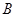 学科合格”的人数为
学科合格”的人数为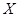 ,求
,求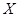 的数学期望.
的数学期望.
附公式与表: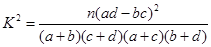
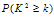 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
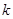 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
如图,三棱锥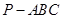 中,
中,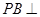 底面
底面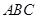 于
于 ,
,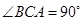 ,
,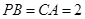 ,点
,点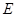 是
是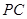 的中点.
的中点.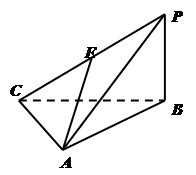
(1)求证:侧面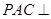 平面
平面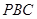 ;
;
(2)若异面直线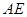 与
与 所成的角为
所成的角为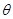 ,且
,且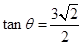 ,
,
求二面角 的大小.
的大小.
椭圆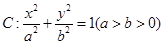 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为 ,点
,点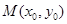 是椭圆C上一点,
是椭圆C上一点,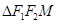 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆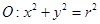 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为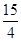 .
.
(1)求椭圆C以及圆O的方程;
(2)当点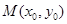 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线 与圆O的位置关系.
与圆O的位置关系.
已知定义在实数集上的函数 ,
,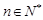 ,其导函数记为
,其导函数记为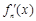 ,
,
(1)设函数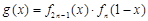 ,求
,求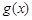 的极大值与极小值;
的极大值与极小值;
(2)试求关于 的方程
的方程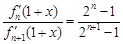 在区间
在区间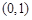 上的实数根的个数。
上的实数根的个数。
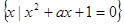 中只有一个元素,则a的值是( ).
中只有一个元素,则a的值是( ). =( )
=( )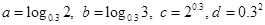 则这四个数的大小关系是( )
则这四个数的大小关系是( )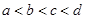


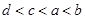
 表示双曲线,则实数k的取值范围是 ( )
表示双曲线,则实数k的取值范围是 ( )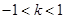
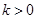

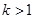 或
或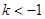
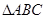 中,角
中,角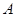 、
、 、
、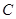 所对的边为
所对的边为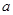 、
、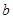 、
、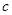 ,若
,若 ,
, ,
,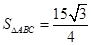 ,则
,则 ( )
( )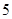

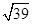

 ,
,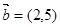 ,
, 满足条件
满足条件  ,则
,则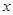 = .
= .
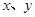 满足
满足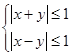 ,则
,则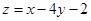 的最大值为
的最大值为 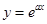 在点
在点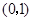 处的切线与直线
处的切线与直线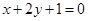 垂直,则
垂直,则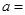 .
.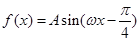 (
(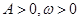 )的部分图像如右所示.
)的部分图像如右所示.
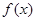 的解析式;
的解析式;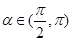 ,且
,且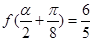 ,求
,求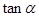 的值.
的值.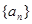 的公差
的公差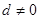 ,等比数列
,等比数列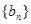 为公比为
为公比为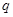 ,且
,且 ,
,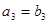 ,
,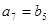 .
. ,是否存在正整数
,是否存在正整数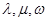 (其中
(其中 )使得
)使得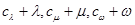 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 粤公网安备 44130202000953号
粤公网安备 44130202000953号