高中数学多面角及多面角的性质解答题

已知函数.
(Ⅰ) 当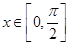时，求函数f(x)的值域；
(Ⅱ)设a,b,c分别为△ABC三个内角A，B，C的对边，f(C)=3,c=1,ab=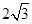，求a,b的值。

(本小题满分12分)
已知向量,，设函数.
（Ⅰ）若函数的零点组成公差为的等差数列，求函数的单调递增区间；
（Ⅱ）若函数的图象的一条对称轴是，（），求函数的值域.

(本题满分13分)
已知函数，若对一切恒成立．求实数的取值范围．

已知函数的最小正周期为,最小值为,图象过点,(1)求的解析式;(2)求满足且的的集合.

(本小题满分12分）
已知函数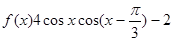
(I)求函数f(x)的最小正周期；
(II)求函数f(x)在区间上的最大值和最小值.

设函数
（1）写出函数的最小正周期及单调递减区间；
（2）当时，函数的最大值与最小值的和为，求不等式的解集．

已知向量
（Ⅰ）求的解析式；
（Ⅱ）求由的图象、轴的正半轴及轴的正半轴三者围成图形的面积。

（本小题满分10分）已知，函数（其中的图像在轴右侧的第一个最高点（即函数取得最大值的点）为，在原点右侧与轴的第一个交点为.
（1）求函数的表达式；
（2）判断函数在区间上是否存在对称轴，存在求出方程；否则说明理由；

（本小题12分）已知
（Ⅰ）若，求使函数为偶函数。
（Ⅱ）在（I）成立的条件下，求满足＝1，∈[－π，π]的的集合。

已知向量，，函数.
（1）求函数的最小正周期和单调增区间；
（2）在中，分别是角的对边，R为外接圆的半径，且，，，且，求的值．

（本小题满分12分）如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为．
（1）求的值； （2）求的值．

已知函数，（其中，x∈R）的最小正周期为．
（1）求ω的值；
（2）设，，，求的值．

(本题满分10分)已知为第三象限角，.
（1）化简；
（2）若，求的值.

已知函数
（Ⅰ）求函数的最小正周期；
（Ⅱ），求函数的最大值及相应的自变量x的取值．

已知
(Ⅰ)若,求的表达式；
（Ⅱ）若函数和函数的图象关于原点对称，求函数的解析式；
（Ⅲ）若在上是增函数，求实数的取值范围.