高中数学几何不等式试题

已知关于的不等式的解集为，则实数的取值范围    ．

定义在R上的运算:x*y=x(1-y),若不等式(x-y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是　　　　. 

“不等式x²-x+m>0在R上恒成立”的一个必要不充分条件是(　　)

A．m>	B．0<m<1
C．m>0	D．m>1

若集合,若集合中的元素个数为,则实数的取值范围为        ．

已知函数f(x)= 则满足不等式f(1-x²)>f(2x)的x的取值范围是　　　　.

设x,y为实数,满足3≤xy²≤8,4≤≤9,则的最大值是　　　. 

集合，若“”是“”的充分条件，则的取值范围是（ ）

A．

B．

C．

D．

“x>0”是“>0”成立的(　　)

A．充分非必要条件	B．必要非充分条件
C．非充分非必要条件	D．充要条件

某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司要生产A类产品至少50件,B类产品至少140件,所需租赁费最多不超过2500元,写出满足上述所有不等关系的不等式.

（本小题满分13分）
在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图所示的路径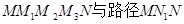都是M到N的“L路径”。某地有三个新建的居民区，分别位于平面xOy内三点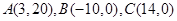处。现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心。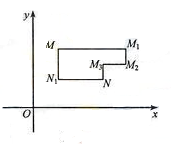

（I）写出点P到居民区A的“L路径”长度最小值的表达式（不要求证明）；
（II）若以原点O为圆心，半径为1的圆的内部是保护区，“L路径”不能进入保护区，请确定点P的位置，使其到三个居民区的“L路径”长度值和最小。

设a，b∈R，定义运算“∧”和“∨”如下：
a∧b＝a∨b＝
若正数a，b，c，d满足ab≥4，c＋d≤4，则(  )

A．a∧b≥2，c∧d≤2	B．a∧b≥2，c∨d≥2
C．a∨b≥2，c∧d≤2	D．a∨b≥2，c∨d≥2

实数a_i（i=1,2,3,4,5,6）满足（a₂－a₁）²+（a₃－a₂）²+（a₄－a₃）²+（a₅－a₄）²+（a₆－a₅）²=1则（a₅+a₆）－（a₁+a₄）的最大值为（　　　）

A．3

B．2

C．

D．1

下列说法：
①命题“”的否定是“”；
②关于的不等式恒成立，则的取值范围是；
③对于函数，则有当时，，使得函数在上有一个零点；
④已知，且是常数，又的最小值是，则.
其中错误的是            ．（填写所有符合题意的序号）

已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.

小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则(　　)

A．a<v<	B．v=
C．<v<	D．v=