已知集合 ,B={x/ax2+bx+c
,B={x/ax2+bx+c 0},若
0},若 则
则 的最小值_______.
的最小值_______.
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.
函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
实数ai(i=1,2,3,4,5,6)满足(a2-a1)2+(a3-a2)2+(a4-a3)2+(a5-a4)2+(a6-a5)2=1则(a5+a6)-(a1+a4)的最大值为( )
| A.3 | B.2 |
C. |
D.1 |
已知f(x)为二次函数,不等式f(x)+2<0的解集是 ,且对任意α、β∈R恒有f(sinα)≤0,f(2+cosβ)≥0,求函数f(x)的解析式.
,且对任意α、β∈R恒有f(sinα)≤0,f(2+cosβ)≥0,求函数f(x)的解析式.
“x>0”是“ >0”成立的( )
>0”成立的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.非充分非必要条件 | D.充要条件 |
若a>b>c,n∈N+,且 恒成立,则n的最大值为( ).
恒成立,则n的最大值为( ).
| A.2 | B.3 | C.4 | D.5 |
已知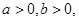 且
且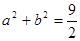 ,若
,若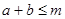 恒成立,
恒成立,
(1)求 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
设a,b∈R,定义运算“∧”和“∨”如下:
a∧b= a∨b=
a∨b=
若正数a,b,c,d满足ab≥4,c+d≤4,则( )
| A.a∧b≥2,c∧d≤2 | B.a∧b≥2,c∨d≥2 |
| C.a∨b≥2,c∧d≤2 | D.a∨b≥2,c∨d≥2 |