设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
)设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)判断 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
当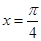 时,函数
时,函数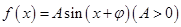 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点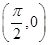 对称 对称 |
B.偶函数且图像关于点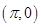 对称 对称 |
C.奇函数且图像关于直线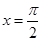 对称 对称 |
D.偶函数且图像关于点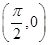 对称 对称 |
请阅读下列材料: 已知一系列函数有如下性质:
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
……
利用上述所提供的信息解决问题:
若函数 的值域是
的值域是 ,则实数
,则实数 的值是 .
的值是 .
已知 是函数
是函数 的两个零点,函数
的两个零点,函数 的最小值为
的最小值为 ,记
,记
(ⅰ)试探求 之间的等量关系(不含
之间的等量关系(不含 );
);
(ⅱ)当且仅当 在什么范围内,函数
在什么范围内,函数 存在最小值?
存在最小值?
(ⅲ)若 ,试确定
,试确定 的取值范围。
的取值范围。
函数 定义如下:对任意
定义如下:对任意 ,当
,当 为有理数时,
为有理数时, ;当
;当 为无理数时,
为无理数时, ;则称函数
;则称函数 为定义在实数上的狄利克雷拓展函数.下列关于函数
为定义在实数上的狄利克雷拓展函数.下列关于函数 说法错误的是( )
说法错误的是( )
A. 的值域为 的值域为 |
B. 是偶函数 是偶函数 |
C. 是周期函数且 是周期函数且 是 是 的一个周期 的一个周期 |
D. 在实数集上的任何区间都不是单调函数 在实数集上的任何区间都不是单调函数 |
为了得到函数 的图像,可将函数
的图像,可将函数 的图像上所有的点的( )
的图像上所有的点的( )
A.纵坐标缩短为原来的 ,横坐标不变,再向右平移1个单位 ,横坐标不变,再向右平移1个单位 |
B.纵坐标缩短为原来的 ,横坐标不变,再向左平移1个单位 ,横坐标不变,再向左平移1个单位 |
| C.横坐标伸长为原来的2倍,纵坐标不变,再向左平移1个单位 |
| D.横坐标伸长为原来的2倍,纵坐标不变,再向右平移1个单位 |
已知函数 是奇函数。
是奇函数。
(1)求实数a的值;
(2)判断函数 在R上的单调性并用定义法证明;
在R上的单调性并用定义法证明;
(3)若函数 的图像经过点
的图像经过点 ,这对任意
,这对任意 不等式
不等式 ≤
≤ 恒成立,求实数m的范围。
恒成立,求实数m的范围。