高中数学函数迭代试题

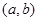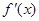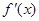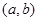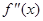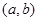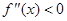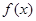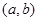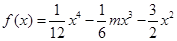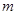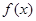设函数在区间上的导函数为，在区间上的导函数为，若在区间上恒成立，则称函数在区间上的“凸函数”。已知，若对任意的实数满足时，函数在区间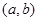上为“凸函数”，则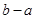的最大值为
Ａ.4           B.3            C. 2           D.1

已知函数，则    ．

定义在［－1，1］上的奇函数满足，且当，时，有．
（1）试问函数f(x)的图象上是否存在两个不同的点A，B，使直线AB恰好与y轴垂直，若存在，求出A，B两点的坐标；若不存在，请说明理由并加以证明.
（2）若对所有，恒成立，
求实数m的取值范围．

.已知函数，则等于    （    ）

A．

B．

C．

D．

已知是定义在上的非负可导函数，且满足，对任意正数，若，则必有（ ）

A．	B．
C．	D．

已知函数
（1）当时，求的解集
（2）若关于的不等式的解集是，求的取值范围

已知函数的定义域为，对于任意的，都有，且当时，.
（1）求证：为奇函数；   （2）求证:是上的减函数；

已知为定义在上的可导函数，且 对于任意恒成立，则（   ）

A．

B．

C．

D．

已知函数的定义域为R，其导函数的图像如图所示，则对于任意，()，下列结论正确的是（  ）

①<0恒成立 ②；③；
④；⑤。

A．①③

B．①③④

C．②④

D．②⑤

若函数f(x)=,若f(a)>f(-a),则实数a的取值范围是（  ）

A．（-1，0）∪（0，1）	B．（-∞，-1）∪（1,+∞）
C．（-1，0）∪（1,+∞）	D．（-∞，-1）∪（0,1）

设f(x)＝ ， g(x)＝ 则f(g())的值为（     ）

A．1

B．0

C．－1

D．

若f(x)＝(m－1)x²＋6mx＋2是偶函数，则f(0)、f(1)、f(－2)从小到大的顺序是__________．

已知函数是定义在R上的奇函数，且当时,不等式成立，若， ，则的大小关系是（   ）

A．

B．

C．

D．

已知函数，下列命题:
①的定义域为；
②是奇函数；
③在单调递增；
④若实数a，b满足，则；
⑤设函数在的最大值为M，最小值为m，则M＋m＝2013
其中真命题的序号是           （写出所有真命题的序号）

已知，直线与函数的图像都相切，且与函数的图像的切点的横坐标为1．  
（1）求直线的方程及的值；
（2）若（其中是的导函数），求函数的最大值；
（3）当时，求证：．