吉林省长春市高中毕业班第三次调研测试文科数学试卷
复数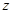 满足
满足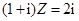 ,则复数
,则复数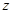 在复平面内对应的点在( )
在复平面内对应的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
如图所示的程序框图,该算法的功能是( )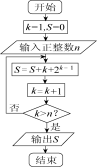
A.计算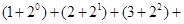 .... ....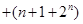 的值 的值 |
B.计算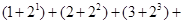 .... ....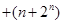 的值 的值 |
C.计算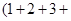 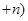 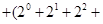 ..... .....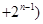 的值 的值 |
D.计算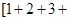 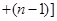 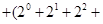 ... ...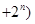 的值 的值 |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知双曲线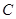 :
: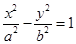
 的焦距为
的焦距为 ,焦点到双曲线
,焦点到双曲线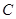 的渐近线的距离为
的渐近线的距离为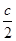 ,则双曲线
,则双曲线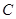 的离心率为( )
的离心率为( )
| A.2 | B. |
C. |
D. |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为( )
A.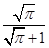 |
B.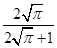 |
C.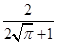 |
D.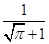 |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知函数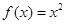 的图象在点
的图象在点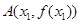 与点
与点 处的切线互相垂直,
处的切线互相垂直,
并交于点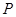 ,则点
,则点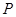 的坐标可能是( )
的坐标可能是( )
A.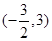 |
B. |
C.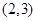 |
D.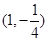 |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知点 ,
, 为圆
为圆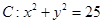 上的任意两点,且
上的任意两点,且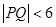 ,若
,若 中点组成的区域为
中点组成的区域为 ,在圆
,在圆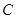 内任取一点,则该点落在区域
内任取一点,则该点落在区域 上的概率为( )
上的概率为( )
A. |
B.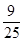 |
C. |
D.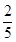 |
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,其可见部分如下,据此解答如下问题:


(1)计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在 之间的概率;
之间的概率;
(3)根据频率分布直方图估计这次测试的平均分.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
如图,直三棱柱 中,
中,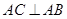 ,
,  ,
,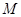 是
是 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点,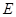 为
为 上一点.
上一点.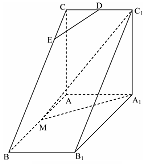
(1)若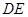 ∥平面
∥平面 ,求
,求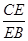 ;
;
(2)平面 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知抛物线 :
: 的焦点为
的焦点为 ,若过点
,若过点 且斜率为
且斜率为 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
.
(1)求抛物线 的方程;
的方程;
(2)设直线 为抛物线
为抛物线 的切线,且
的切线,且 ∥
∥ ,
, 为
为 上一点,求
上一点,求 的最小值.
的最小值.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知函数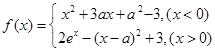 ,
, .
.
(1)若函数 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)若函数 的图象上存在两点关于原点对称,求
的图象上存在两点关于原点对称,求 的范围.
的范围.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
如图,圆 与圆
与圆 交于
交于 两点,以
两点,以 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆 和圆
和圆 于
于 两点,延长
两点,延长 交圆
交圆 于点
于点 ,延长
,延长 交圆
交圆 于点
于点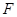 .已知
.已知 .
.
(1)求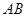 的长;
的长;
(2)求 .
.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
已知曲线 的参数方程为
的参数方程为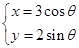 (
(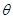 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程;
的普通方程;
(2)若点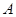 在曲线
在曲线 上,点
上,点
 ,当点
,当点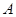 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点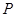 的轨迹方程.
的轨迹方程.
来源:2014届吉林省长春市高中毕业班第三次调研测试文科数学试卷
 ,集合
,集合 ,则集合
,则集合 中有___个元素
中有___个元素 上单调递减,并且是偶函数的是( )
上单调递减,并且是偶函数的是( )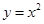
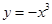
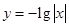
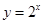
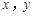 之间关系最强的是( )
之间关系最强的是( )
 各角的对应边分别为
各角的对应边分别为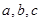 ,满足
,满足
 ,则角
,则角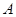 的范围是( )
的范围是( )
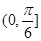

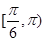
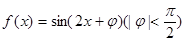 的图象向左平移
的图象向左平移 个单位后关于原点对称,则函
个单位后关于原点对称,则函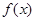 在
在 上的最小值为( )
上的最小值为( )
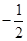
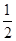

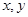 满足:
满足: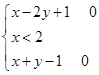 ,
,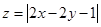 ,则
,则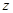 的取值范围是( )
的取值范围是( )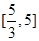
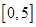
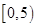
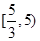
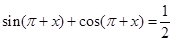 ,则
,则 .
. ,则
,则 .
.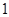 ,则圆锥的体积为 .
,则圆锥的体积为 . 中,已知点
中,已知点 的坐标为
的坐标为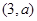 ,
,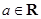 ,点
,点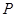 满足
满足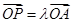 ,
,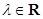 ,
, ,则线段
,则线段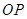 在
在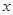 轴上的投影长度的最大值为 .
轴上的投影长度的最大值为 . 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
. .
.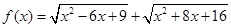 .
. 的解集;
的解集;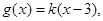
 ,若
,若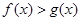 对任意的
对任意的 都成立,求
都成立,求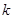 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号