下列各组函数中表示同一函数的是 ( )
A.f(x)=x与g(x)=( )2 )2 |
B.f(x)=|x|与g(x)= |
C.f(x)= 与g(x)= 与g(x)= |
D.f(x)= 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |
设 在区间
在区间 上有定义, 若
上有定义, 若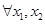
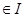 , 都有
, 都有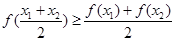 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若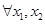
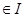 , 都有
, 都有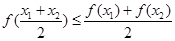 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则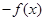 是区间
是区间 的向下凸函数;
的向下凸函数;
②若 和
和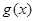 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则 是区间
是区间 的向上凸函数;
的向上凸函数;
③若 在区间
在区间 的向下凸函数且
的向下凸函数且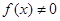 ,则
,则 是区间
是区间 的向上凸函数;
的向上凸函数;
④若 是区间
是区间 的向上凸函数,
的向上凸函数, , 则有
, 则有

其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对任意
对任意 恒成立.
恒成立.
(Ⅰ)如果p是真命题,求实数 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题且“p且q”为假命题,求实数 的取值范围.
的取值范围.
如果函数 对于区间D内任意的
对于区间D内任意的 ,有
,有

 成立,称
成立,称 是区间D上的“凸函数”.已知函数
是区间D上的“凸函数”.已知函数 在区间
在区间 上是 “凸函数”,则在△
上是 “凸函数”,则在△ 中,
中, 的最大值是( )
的最大值是( )
A. |
B. |
C. |
D. |
若存在实常数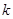 和
和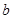 ,使得函数
,使得函数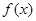 和
和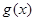 对其定义域上的任意实数
对其定义域上的任意实数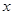 分别满足:
分别满足: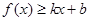 和
和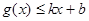 ,则称直线
,则称直线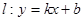 为
为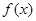 和
和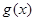 的“隔离直线”.已知
的“隔离直线”.已知 ,
,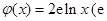 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求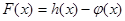 的极值;
的极值;
(Ⅱ)函数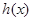 和
和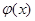 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
设甲、乙两地的距离为a(a>0),小王骑自行车以匀速从甲地到乙地用了20min,在乙地休息10min后,他又以匀速从乙地返回到甲地用了30min,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图像为( )