高中数学函数迭代试题

设函数，其中为常数．
（Ⅰ）当时，判断函数在定义域上的单调性；
（Ⅱ）当时,求的极值点并判断是极大值还是极小值；
（Ⅲ）求证对任意不小于3的正整数，不等式都成立．

下列关于函数、函数的定义域、函数的值域、函数的对应法测的结构图正确的是

已知函数
(1)解关于的不等式
(2)若，的解集非空，求实数m的取值范围

定义在R上的函数y=f（x）是增函数，且函数y=f（x－3）的图象关于点（3，0）成中心对称，若s，t满足f（s－2s） ≥－f（2t－t），则

A．s≥t

B．s<t

C．|s－1|≥|t－1|

D．s+t≥0

若函数是定义在上的奇函数，在上为减函数，且，则使得的的取值范围是     (     )

A．	B．
C．	D．

设函数,观察:,，，, ……根据以上事实，由归纳推理可得当N^*且时,                                       ( 　　)

A．

B．

C．

D．

已知函数的零点依次为，则（   ）

A．

B．

C．

D．

是定义在上的奇函数，且当，设，给出三个条件：①②，③．其中可以推出的条件共有          个．

设偶函数对任意都有，且当时，,则        ．

设，函数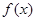的图像与函数的图像关于点对称．
（1）求函数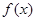的解析式；
（2）若关于的方程有两个不同的正数解，求实数的取值范围．

若f(x)＝(m－1)x²＋6mx＋2是偶函数，则f(0)、f(1)、f(－2)从小到大的顺序是__________．

已知函数，
（1）若函数满足，且在定义域内恒成立，求实数的取值范围；
（2）若函数在定义域上是单调函数，求实数的取值范围；

函数的零点的个数为     ．

对于函数，若，则称为函数的“不动点”；若，则称为函数的“稳定点”.如果函数的“稳定点”恰是它的“不动点”，那么实数的取值范围是（    ）

A．

B．

C．

D．

已知函数，则    ．