[福建]2013届福建省三明市普通高中毕业班5月质量检查理科数学试卷
阅读下边程序框图,下列说法正确的是 ( )
| A.该框图只含有顺序结构、条件结构 |
| B.该框图只含有顺序结构、循环结构 |
| C.该框图只含有条件结构、循环结构 |
| D.该框图包含顺序结构、条件结构、循环结构 |
已知函数 ,则
,则 是 ( )
是 ( )
| A.非奇非偶函数,且在(0,+∞)上单调递增 |
B.奇函数,且在 上单调递增 上单调递增 |
| C.非奇非偶函数,且在(0,+∞)上单调递减 |
D.偶函数,且在 上单调递减 上单调递减 |
在 中,“
中,“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
过双曲线
 ,
, 的左焦点
的左焦点 作圆
作圆 :
:  的两条切线,切点为
的两条切线,切点为 ,
, ,双曲线左顶点为
,双曲线左顶点为 ,若
,若 ,则双曲线的渐近线方程为 ( )
,则双曲线的渐近线方程为 ( )
A. |
B. |
C. |
D. |
对于函数 ,若
,若 ,则称
,则称 为函数
为函数 的“不动点”;若
的“不动点”;若 ,则称
,则称 为函数
为函数 的“稳定点”.如果函数
的“稳定点”.如果函数 的“稳定点”恰是它的“不动点”,那么实数
的“稳定点”恰是它的“不动点”,那么实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 ,(
,( ,
, .若
.若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,并在
对称,并在 处取得最小值,则正实数
处取得最小值,则正实数 的值构成的集合是 .
的值构成的集合是 .
如图,在几何体 中,
中, 平面
平面 ,
, ,
, 是等腰直角三角形,
是等腰直角三角形, ,且
,且 ,点
,点 是
是 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求 的分布列及数学期望.
的分布列及数学期望.
已知椭圆 的离心率为
的离心率为 ,且椭圆
,且椭圆 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)如图,设直线 与椭圆
与椭圆 交于
交于 两点(其中点
两点(其中点 在第一象限),且直线
在第一象限),且直线 与定直线
与定直线 交于点
交于点 ,过
,过 作直线
作直线 交
交 轴于点
轴于点 ,试判断直线
,试判断直线 与椭圆
与椭圆 的公共点个数.
的公共点个数.
某企业有两个生产车间,分别位于边长是 的等边三角形
的等边三角形 的顶点
的顶点 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
(Ⅰ)按下列要求确定函数关系式:
①设 长为
长为 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中一个合适的函数关系式,求总路程  的最小值,并指出点
的最小值,并指出点 的位置.
的位置.
已知函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,在曲线
时,在曲线 上是否存在两点
上是否存在两点 ,使得曲线在
,使得曲线在 两点处的切线均与直线
两点处的切线均与直线 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
(Ⅲ)若 在区间
在区间 存在最大值
存在最大值 ,试构造一个函数
,试构造一个函数 ,使得
,使得 同时满足以下三个条件:①定义域
同时满足以下三个条件:①定义域 ,且
,且 ;②当
;②当 时,
时, ;③在
;③在 中使
中使 取得最大值
取得最大值 时的
时的 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数 即可)
即可)
已知矩阵 ,绕原点逆时针旋转
,绕原点逆时针旋转 的变换所对应的矩阵为
的变换所对应的矩阵为 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)若曲线 :
: 在矩阵
在矩阵 对应变换作用下得到曲线
对应变换作用下得到曲线 ,求曲线
,求曲线 的方程.
的方程.
在平面直角坐标系 中,以坐标原点
中,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 为参数,
为参数, ).
).
(Ⅰ)化曲线 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(Ⅱ)若直线 经过点
经过点 ,求直线
,求直线 被曲线
被曲线 截得的线段
截得的线段 的长.
的长.
 ”的否定是 ( )
”的否定是 ( )



 (其中
(其中 为虚数单位),则复数
为虚数单位),则复数 的共轭复数
的共轭复数 是 ( )
是 ( )



 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 等于 ( )
等于 ( ) 的最小正周期是 ( )
的最小正周期是 ( )








 ,若
,若 ,则
,则 .
. 上一点
上一点 到焦点
到焦点 的距离为4,则点
的距离为4,则点 )6的展开式中, 常数项是 .
)6的展开式中, 常数项是 . ,
, ,曲线
,曲线 及
及 轴所围成的图形的面积是 .
轴所围成的图形的面积是 .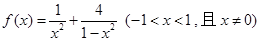 .
.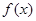 的最小值;
的最小值;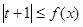 恒成立,求实数
恒成立,求实数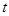 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号