今年我国部分省市出现了人感染H7N9禽流感确诊病例，各地家禽市场受其影响生意冷清．A市虽未发现H7N9疑似病例，但经抽样有20%的市民表示还会购买本地家禽．现将频率视为概率，解决下列问题：
（Ⅰ）从该市市民中随机抽取3位，求至少有一位市民还会购买本地家禽的概率；
（Ⅱ）从该市市民中随机抽取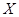
位，若连续抽取到两位愿意购买本地家禽的市民，或抽取的人数达到4位，则停止抽取，求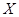的分布列及数学期望．
相关试题
是R上的减函数，命题q：函数
在
的值域为
，若“p且q”为假命题，“p或q”为真命题，求
的取值范围.
，分别根据下列条件，求实数
的取值范围（1）
(2)
．
的图像在
处的切线方程；
，求函数
在
上的最大值.
，都有
成立．
在
及
时取得极值．（Ⅰ）求a、b的值；（Ⅱ）若对于任意的
，都有
成立，求c的取值范围．推荐套卷
今年我国部分省市出现了人感染H7N9禽流感确诊病例，各地家禽市场受其影响生意冷清．A市虽未发现H7N9疑似病例，但经抽样有20%的市民表示还会购买本地家禽．现将频率视为概率，解决下列问题：
（Ⅰ）从该市市民中随机抽取3位，求至少有一位市民还会购买本地家禽的概率；
（Ⅱ）从该市市民中随机抽取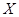位，若连续抽取到两位愿意购买本地家禽的市民，或抽取的人数达到4位，则停止抽取，求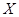的分布列及数学期望．
粤公网安备 44130202000953号