某企业有两个生产车间,分别位于边长是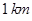 的等边三角形
的等边三角形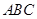 的顶点
的顶点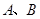 处(如图),现要在边
处(如图),现要在边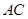 上的
上的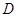 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返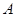 车间5次,往返
车间5次,往返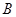 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为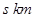 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)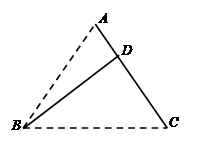
(Ⅰ)按下列要求确定函数关系式:
①设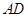 长为
长为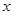 ,将
,将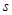 表示成
表示成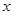 的函数关系式;
的函数关系式;
②设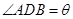 ,将
,将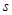 表示成
表示成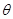 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中一个合适的函数关系式,求总路程 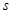 的最小值,并指出点
的最小值,并指出点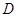 的位置.
的位置.
推荐套卷
某企业有两个生产车间,分别位于边长是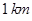 的等边三角形
的等边三角形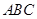 的顶点
的顶点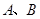 处(如图),现要在边
处(如图),现要在边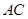 上的
上的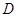 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返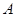 车间5次,往返
车间5次,往返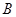 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为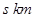 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)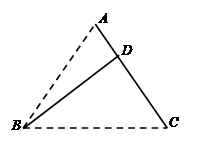
(Ⅰ)按下列要求确定函数关系式:
①设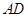 长为
长为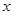 ,将
,将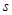 表示成
表示成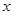 的函数关系式;
的函数关系式;
②设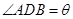 ,将
,将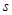 表示成
表示成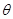 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中一个合适的函数关系式,求总路程 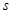 的最小值,并指出点
的最小值,并指出点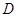 的位置.
的位置.