定义在[-1,1]上的奇函数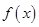 满足
满足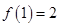 ,且当
,且当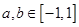 ,
, 时,有
时,有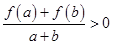 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有
对所有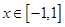 ,
,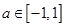 恒成立,
恒成立,
求实数m的取值范围.
相关知识点
推荐套卷
定义在[-1,1]上的奇函数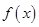 满足
满足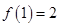 ,且当
,且当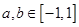 ,
, 时,有
时,有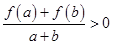 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有
对所有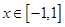 ,
,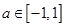 恒成立,
恒成立,
求实数m的取值范围.