设 在区间
在区间 上有定义, 若
上有定义, 若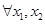
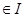 , 都有
, 都有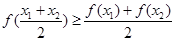 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若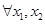
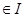 , 都有
, 都有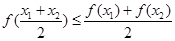 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则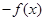 是区间
是区间 的向下凸函数;
的向下凸函数;
②若 和
和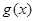 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则 是区间
是区间 的向上凸函数;
的向上凸函数;
③若 在区间
在区间 的向下凸函数且
的向下凸函数且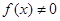 ,则
,则 是区间
是区间 的向上凸函数;
的向上凸函数;
④若 是区间
是区间 的向上凸函数,
的向上凸函数, , 则有
, 则有

其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
关于函数 ,有下列结论:①函数
,有下列结论:①函数 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数 是奇函数;③函数
是奇函数;③函数 的最小值为-
的最小值为- ;④当
;④当 时,函数
时,函数 是增函数;当
是增函数;当 时,函数
时,函数 是减函数.
是减函数.
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
当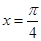 时,函数
时,函数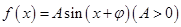 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点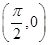 对称 对称 |
B.偶函数且图像关于点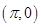 对称 对称 |
C.奇函数且图像关于直线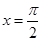 对称 对称 |
D.偶函数且图像关于点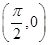 对称 对称 |
若函数 都在区间
都在区间 上有定义,对任意
上有定义,对任意 ,都有
,都有 成立,则称函数
成立,则称函数 为区间
为区间 上的“伙伴函数”
上的“伙伴函数”
(1)若 为区间
为区间 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?
(3)若 为区间
为区间 上的“伙伴函数”,求
上的“伙伴函数”,求 的取值范围
的取值范围
已知函数 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表:
 |
1 |
2 |
3 |
4 |
5 |
 |
 |
 |
1 |
4 |
7 |
在下列区间中,函数 必有零点的区间为( ).
必有零点的区间为( ).
A.(1,2) B. (2,3) C.(3,4) D. (4,5)
设函数 ,观察:
,观察: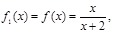
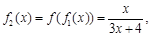

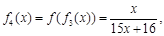
……根据以上事实,由归纳推理可得:
当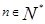 且
且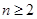 时,
时,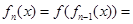 .
.