[河南]2013届河南省中原名校高三下学期第二次联考理科数学试卷
甲乙丙3位同学选修课程,从4门课程中选。甲选修2门,乙丙各选修3门,则不同的选修方案共有
| A.36种 | B.48种 | C.96种 | D.1 92种 |
从一个正方体中截去部分几何体,得到的几何体三视图如下,则此几何体的体积是( )
| A.64 | B. |
C. |
D. |
执行如图所示的程序框图,若输出a= 341,判断框内应填写( )
| A.k < 4? | B.k < 5? |
| C.k< 6? | D.k < 7? |
若A为不等式组 所示的平面区域,则当a从-2连续变化到1时,动直线x+ y =a扫过A中的那部分区域面积为( )
所示的平面区域,则当a从-2连续变化到1时,动直线x+ y =a扫过A中的那部分区域面积为( )
| A.2 | B.1 |
C. |
D. |
已知过抛物线y2 =2px(p>0)的焦点F的直线x-my+m=0与抛物线交于A,B两点,且△OAB(O为坐标原点)的面积为2 ,则m6+ m4的值为( )
,则m6+ m4的值为( )
| A.1 | B. 2 | C.3 | D.4 |
平行四边形ABCD中, ·
· =0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
A. |
B. |
C. |
D. |
已知R上的函数y=f(x),其周期为2,且x∈(-1,1]时f(x)=1+x2,函数g(x)= ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| A.11 | B.10 | C.9 | D.8 |
下列若干命题中,正确命题的序号是 。
①“a=3”是直线ax+2y+2a=0和直线3x+(a一l)y一a+7 =0平行的充分不必要条件;
②△ABC中,若 ,则该三角形形状为等腰三角形;
,则该三角形形状为等腰三角形;
③两条异面直线在同一平面内的投影可能是两条互相垂直的直线;
④对于命题 使得
使得 ,则
,则 均有
均有 .
.
已知等差数列 中,首项a1=1,公差d为整数,且满足
中,首项a1=1,公差d为整数,且满足 数列
数列 满足
满足 前
前 项和为
项和为 .
.
(1)求数列 的通项公式an;
的通项公式an;
(2)若S2为 ,
, 的等比中项,求正整数m的值.
的等比中项,求正整数m的值.
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
0.1 |
0.4 |
0.3 |
0.1 |
0.1 |
从第—个车主开始预约登记时计时(用频率估计概率),
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD =3.BD=CD=2.
(1)求证:AD⊥BC;
(2)求二面角B—AC—D的余弦值.
若椭圆 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量 为方向向量的直线
为方向向量的直线 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。
(2)设M,N为椭圆上的两个动点, ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
已知函数f(x)=1n(2ax+1)+ -x2-2ax(a∈R).
-x2-2ax(a∈R).
(1)若y=f(x)在[4,+∞)上为增函数,求实数a的取值范围;
(2)当a= 时,方程f(1-x)=
时,方程f(1-x)= 有实根,求实数b的最大值.
有实根,求实数b的最大值.
如图,△ABC内接于⊙O,AB =AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB =6,BC =4,求AE.
坐标系与参数方程在直角坐标系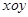 中,直线
中,直线 的参数方程为
的参数方程为 (t 为参数)。在极坐标系(与直角坐标系
(t 为参数)。在极坐标系(与直角坐标系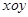 取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为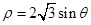 。
。
(1)求圆C的直角坐标方程;
(2)设圆C与直线 交于点A,B,若点P的坐标为(2,
交于点A,B,若点P的坐标为(2,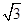 ),求|PA|+|PB|.
),求|PA|+|PB|.
 (
( 为虚数单位),则
为虚数单位),则 的虚部为
的虚部为 ,则下列不正确的是
,则下列不正确的是



 .则函数
.则函数 的图像的一条对称轴方程为
的图像的一条对称轴方程为


 则
则





 ,则
,则 的大小关系
的大小关系



 的展开式中常数项的值是 (数字作答);
的展开式中常数项的值是 (数字作答); 的图像在点
的图像在点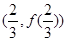 处的切线斜率是 ;
处的切线斜率是 ;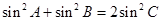 ,则∠C最大值为_ ;
,则∠C最大值为_ ; ,g(x)=2|x|+a.
,g(x)=2|x|+a. 粤公网安备 44130202000953号
粤公网安备 44130202000953号