高中数学函数迭代试题

设函数,观察: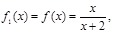




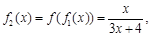
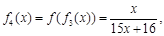
……根据以上事实，由归纳推理可得：
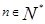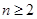当且时，                 .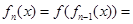

已知函数是R上的奇函数，若对于，都有，
时，的值为（  ）

A．

B．

C．1

D．2

已知不等式，
（1）若对所有的实数不等式恒成立，求的取值范围；
（2）设不等式对于满足的一切的值都成立，求的取值范围。

已知函数，则，，的大小关系为

A．	B．
C．	D．

函数y＝－2sin x的图象大致是（　　）

已知，若关于的方程有实根，则的取值范围是____.

与函数y=|x|有相同图像的一个函数是(    )

A．y=

B．y=a

C．y=

D．y=log5x

已知奇函数在上是增函数，且
① 确定函数的解析式；
② 解不等式＜0.

观察，，，由归纳推理可得：若定义在R上的函数满足=，记为的的导函数,则=(    )

A．

B．

C．

D．

已知函数，
（1）若函数满足，且在定义域内恒成立，求实数的取值范围；
（2）若函数在定义域上是单调函数，求实数的取值范围；

设f（x）=log（）为奇函数，a为常数．
（Ⅰ）求a的值；
（Ⅱ）证明f（x）在（1，+∞）内单调递增；
（Ⅲ）若对于［3，4］上的每一个的值，不等式恒成立，求实数的取值范围.

设则不等式的解集为（  ）

A．(1，2)∪(3，+∞)	B．(，+∞)
C．(1，2)∪(，+∞)	D．(1，2)

已知函数是定义在上的奇函数，且当时，不等式成立，若，，，则a，b，c间的大小关系是(　　)．

A．a＞b＞c

B．c＞b＞a

C．c＞a＞b

D．a＞c＞b

已知函数．若关于的不等式的解集非空，则实数的取值范围是________．

设函数是定义域为的奇函数．
(Ⅰ)求的值；
(Ⅱ)若，且在上的最小值为，求的值.