高中数学函数迭代解答题

证明函数f(x)＝x＋在(0,1)上为减函数.

已知函数，．
（Ⅰ）判定在上的单调性；
（Ⅱ）求在上的最小值；
（Ⅲ）若， ，求实数的取值范围．

已知定义域为的函数对任意实数满足
，且.
（1）求及的值；
（2）求证：为奇函数且是周期函数.

已知函数 .
(1) 求函数的定义域;
(2) 求证在上是减函数;
(3) 求函数的值域.

已知函数．
(1)判断函数的奇偶性，并加以证明；
(2)用定义证明在上是减函数；
(3)函数在上是单调增函数还是单调减函数？(直接写出答案，不要求写证明过程)．

已知是定义在上的奇函数，当时，。
（1）求函数的解析式；
（2）画出函数的图象，并求函数的单调区间；
（3）当为何值时，方程有三个解？

已知函数是定义在上的减函数，且，求实数的取值范围。

设函数
（1）证明：当时， 
（2）设当时，，求的取值范围。

设为实数，函数。
（1）若，求的取值范围    （2）求的最小值     
（3）设函数，直接写出（不需要给出演算步骤）不等式的解集。

已知函数，（且）。
（1）设，令，试判断函数在上的单调性并证明你的结论；
（2）若且的定义域和值域都是，求的最大值；
（3）若不等式对恒成立，求实数的取值范围；

已知函数
（1）
（2）

已知函数f(x)是定义在（0，+∞）上的单调增函数，满足f(xy)=f(x)+f(y),f(3)=1
（1）求f(1)的值
（2）若满足f(x) +f(x-8)≤2 求x的取值范围

设a∈R，函数f(x)＝lnx－ax.
（1）讨论函数f(x)的单调区间和极值；
（2）已知（e为自然对数的底数）和x₂是函数f(x)的两个不同的零点，求a的值并证明：x₂＞e.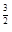

已知函数
(1)若不等式的解集为求实数的值
(2)在(1)的条件下若对一切实数恒成立求实数的
取值范围

已知函数．
（1）若函数f（x）的图象在处的切线斜率为3，求实数m的值；
（2）求函数f（x）的单调区间；
（3）若函数在[1，2]上是减函数，求实数m的取值范围．