已知函数 ,且
,且 在
在 处取得极值.
处取得极值.
(1)求 的值;
的值;
(2)若当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)对任意的 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
已知函数
(1)若 ,求函数
,求函数 在点(0,
在点(0, )处的切线方程;
)处的切线方程;
(2)是否存在实数 ,使得
,使得 的极大值为3.若存在,求出
的极大值为3.若存在,求出 值;若不存在,说明理由。
值;若不存在,说明理由。
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
(Ⅰ)写出所有可能的数对( ,并计算
,并计算 ,且
,且 的概率;
的概率;
(Ⅱ)求函数 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
= .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数 ,并求使得函数
,并求使得函数 有零点的实数
有零点的实数 的取值范围.
的取值范围.
如果函数 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“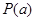 性质”.
性质”.
(1)判断函数 是否具有“
是否具有“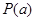 性质”,若具有“
性质”,若具有“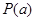 性质”求出所有
性质”求出所有 的值;若不具有“
的值;若不具有“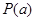 性质”,请说明理由.
性质”,请说明理由.
(2)已知 具有“
具有“ 性质”,且当
性质”,且当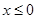 时
时 ,求
,求 在
在 上的最大值.
上的最大值.
(3)设函数 具有“
具有“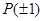 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013个,求
交点个数为2013个,求 的值.
的值.
已知函数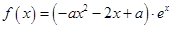 ,
,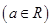
(1)当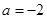 时,求函数
时,求函数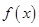 的极值;
的极值;
(2) 若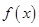 在[-1,1]上单调递减,求实数
在[-1,1]上单调递减,求实数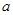 的取值范围.
的取值范围.
(本小题满分13分)已知函数 ,
, .
.
(Ⅰ)设 (其中
(其中 是
是 的导函数),求
的导函数),求 的最大值;
的最大值;
(Ⅱ)求证: 当 时,有
时,有 ;
;
(Ⅲ)设 ,当
,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的最大值.
的最大值.
已知函数f(x)在(-1,1)上有定义,f( )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f( ),试证明:
),试证明:
(1)f(x)为奇函数;
(2)f(x)在(-1,1)上单调递减.