高中数学函数迭代试题

已知函数 $f\left(x\right)=2-\left|x\right|$,无穷数列 $\left\{a_n\right\}$满足 $a_{n+1}=f\left(a_n\right)$, $n\in N^{*}$.
（1）若 $a_1=0$,求 $a_2,a_3,a_4$；
（2）若 $a_1>0$,且 $a_1,a_2,a_3$成等比数列，求 $a_1$的值
（3）是否存在 $a_1$，使得 $a_1,a_2,\cdots ,a_n,\cdots$成等差数列？若存在，求出所有这样的 $a_1$，若不存在，说明理由．

设函数 $f\left(x\right)=e^x+x-2,g\left(x\right)=\ln x+x^2-3$. 若实数 $a,b$满足 $f\left(a\right)=0,f\left(b\right)=0$, 则（   ）

A．	$g\left(a\right)<0<f\left(b\right)$	B．	$f\left(b\right)<0<g\left(a\right)$
C．	$0<g\left(a\right)<f\left(b\right)$	D．	$f\left(b\right)<g\left(a\right)<0$

(1)已知函数为有理数且)，求函数的最小值;
(2)①试用(1)的结果证明命题：设为有理数且，若时，则；
②请将命题推广到一般形式，并证明你的结论；
注：当为正有理数时，有求导公式

已知，且方程无实数根，下列命题：
①方程也一定没有实数根；
②若，则不等式对一切实数都成立；
③若，则必存在实数，使
④若，则不等式对一切实数都成立．
其中正确命题的序号是          ．

已知 $f\left(x\right)$是定义在 $R$上的奇函数. 当 $x>0$时， $f\left(x\right)=x^2-4x$，则不等式 $f\left(x\right)>x$的解集用区间表示为.

设函数 $f\left(x\right)=ax-(1+a)x^2$，其中 $a>0$，区间 $I=\left\{x\left|f\right(x)>0\right\}$

（Ⅰ）求 $I$的长度（注：区间 $(\alpha ,\beta )$的长度定义为 $\beta -\alpha$）；
（Ⅱ）给定常数 $k\in (0,1)$，当 $1-k\le a\le 1+k$时，求 $I$长度的最小值.

若函数 $f\left(x\right)=x^3+a{x}^2+bx+c$有极值点 $x_1$, $x_2$，且 $f\left(x_1\right)=x_1$，则关于 $x$的方程 $3\left(f\right(x){)}^2+2af(x)+b=0$的不同实根个数是（  ）

A．	3	B．	4
C．	5	D．	6

函数 $y=f\left(x\right)$的图像如图所示，在区间 $\left[a,b\right]$上可找到 $n\left(n\ge 2\right)$个不同的数 $x_1,x_2,\dots ,x_n$_，使得 $\frac{f\left(x_1\right)}{x_1}=\frac{f\left(x_2\right)}{x_2}=\dots =\frac{f\left(x_n\right)}{x_n}$，则 $n$的取值范围为（）

A．	$\left\{2,3\right\}$	B．	$\left\{2,3,4\right\}$
C．	$\left\{3,4\right\}$	D．	$\left\{3,4,5\right\}$

下列函数中，既是偶函数又在区间 $\left(0,+\infty \right)$上单调递减的是（）

A．

$y=\frac{1}{x}$

B．

$y=e^{-x}$

C．

$y=-x^2+1$

D．

$y=lg\left|x\right|$

设函数 $f\left(x\right)\mathrm{的定义域为}R，x_0\left(x_0\ne 0\right)是f\left(x\right)\mathrm{的极大值点}，\mathrm{以下结论}$一定正确的是（）

A．	$\forall x\in R,f\left(x\right)\le f\left(x_0\right)$	B．	$-x_0是f\left(-x\right)\mathrm{的极小值点}$
C．	$-x_0是-f\left(x\right)\mathrm{的极小值点}$	D．	$-x_0是-f\left(-x\right)\mathrm{的极小值点}$

正弦曲线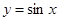通过坐标变换公式，变换得到的新曲线为

A．

B．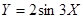

C．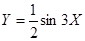

D．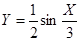

设，则      

已知函数f(x)＝－x²＋2ax＋1－a在x∈[0,1]时有最大值2，求a的值．

若，则                     ;

已知.
（1）若a=0时，求函数在点（1，）处的切线方程；
（2）若函数在[1，2]上是减函数，求实数a的取值范围；
（3）令是否存在实数a，当是自然对数的底）时，函数 的最小值是3，若存在，求出a的值；若不存在，说明理由.