[江西]2012-2013学年江西省景德镇市高二下学期期末考试文科数学试卷

设i是虚数单位，则复数的虚部为（     ）

A．1

B．

C．2

D．

已知集合，，则为(  )

A．

B．

C．

D．

给出如下四个命题
①若“且”为假命题，则、均为假命题
②命题“若”的否命题为“若”
③“任意”的否定是“存在”
④在ABC中，“”是“”的充要条件
其中正确的命题的个数是（ ）

一名小学生的年龄和身高（单位：cm)的数据如下：

由散点图可知，身高y与年龄x之间的线性回归直线方程为，预测该学生10岁时的身高为(    )
A． 154     B． 153 C． 152     D． 151

甲、乙两人在相同条件下进行射击，甲射中目标的概率为,乙射中目标的概率为，两人各射击1次，那么甲、乙至少有一个射中目标的概率为(    )

A．

B．

C．

D．

在下列图象中，二次函数y=ax²+bx与指数函数y=（）^x的图象只可能是（    ）

在中，角A，B，C所对边分别为a,b,c，且，面积，则等于

A．

B．5

C．

D．25

已知数列{}满足，且，则的值是

A．

B．

C．5

D．

若函数，又，且的最小值为，则正数的值是（　　）

A．

B．

C．

D．

已知是周期为的函数，当x∈（）时，设则

如下图，在平面直角坐标系xOy中，锐角和钝角的终边分别与单位圆交于，两点．若点的横坐标是，点的纵坐标是，则的值是___________.

已知某算法的流程图如图所示，则程序运行结束时输出的结果为      ．

函数在区间上最大值与最小值的和为           

已知数列是等差数列，数列是等比数列，则的值为     .

函数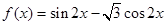 (x∈R)的图象为C,以下结论中:
①图象C关于直线对称;   ②图象C关于点对称;
③函数f(x)在区间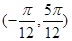内是增函数; 
④由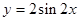的图象向右平移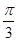个单位长度可以得到图象C.
则正确的是        .(写出所有正确结论的编号)

设对于任意实数x，不等式|x＋7|＋|x－1|≥m恒成立．
(1)求m的取值范围；
(2)当m取最大值时，解关于x的不等式|x－3|－2x≤2m－12.

设函数f (x) ＝.
（1）求f（x）的最小正周期及其图象的对称轴方程；
（2）将函数f（x）的图象向右平移个单位长度，得到函数g(x)的图象，求g (x)在区间上的值域．

从集合中任取三个元素构成三元有序数组，规定 .
（1）从所有的三元有序数组中任选一个，求它的所有元素之和等于10的概率
（2）定义三元有序数组的“项标距离”为（其中），从所有的三元有序数组中任选一个，求它的“项标距离”d为偶数的概率.

设数列为等差数列，且a₃=5，a₅=9；数列的前n项和为S_n，且S_n+b_n=2．    
（1）求数列，的通项公式；
（2）若为数列的前n项和，求．  

设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x.
（1）求f(π)的值； 
（2）当－4≤x≤4时，求f(x)的图象与x轴所围成图形的面积；
（3）写出(－∞，＋∞)内函数f(x)的单调区间．

已知.
（1）若a=0时，求函数在点（1，）处的切线方程；
（2）若函数在[1，2]上是减函数，求实数a的取值范围；
（3）令是否存在实数a，当是自然对数的底）时，函数 的最小值是3，若存在，求出a的值；若不存在，说明理由.