从集合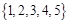 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组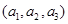 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组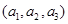 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
推荐套卷
从集合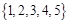 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组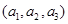 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组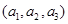 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.