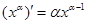(1)已知函数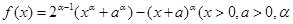 为有理数且
为有理数且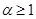 ),求函数
),求函数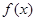 的最小值;
的最小值;
(2)①试用(1)的结果证明命题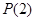 :设
:设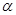 为有理数且
为有理数且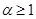 ,若
,若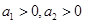 时,则
时,则 ;
;
②请将命题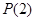 推广到一般形式
推广到一般形式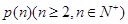 ,并证明你的结论;
,并证明你的结论;
注:当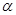 为正有理数时,有求导公式
为正有理数时,有求导公式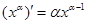
相关知识点
推荐套卷
(1)已知函数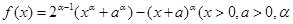 为有理数且
为有理数且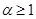 ),求函数
),求函数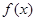 的最小值;
的最小值;
(2)①试用(1)的结果证明命题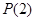 :设
:设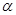 为有理数且
为有理数且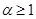 ,若
,若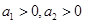 时,则
时,则 ;
;
②请将命题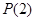 推广到一般形式
推广到一般形式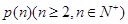 ,并证明你的结论;
,并证明你的结论;
注:当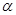 为正有理数时,有求导公式
为正有理数时,有求导公式