如果有穷数列 满足条件:
满足条件: 即
即 ,
, 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得 依次为该数列中连续的前
依次为该数列中连续的前 项,则数列
项,则数列 的前2009项和
的前2009项和 所有可能的取值的序号为
所有可能的取值的序号为
①
②
③
④
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
有限数列D: ,
, ,…,
,…, ,其中
,其中 为数列D的前
为数列D的前 项和,定义
项和,定义 为D的“德光和”,若有
为D的“德光和”,若有 项的数列
项的数列 ,
, ,…,
,…, 的“德光和”为
的“德光和”为 ,则有
,则有 项的数列8,
项的数列8, ,
, ,…,
,…, 的“德光和”为
的“德光和”为
对于一个有限数列 ,定义
,定义 的蔡查罗和(蔡查罗是一位数学家)为
的蔡查罗和(蔡查罗是一位数学家)为 ,其中
,其中 .若一个99项的数列(
.若一个99项的数列( 的蔡查罗和为1000,那么100项数列
的蔡查罗和为1000,那么100项数列 的蔡查罗和为( )
的蔡查罗和为( )
| A.993 | B.995 | C.997 | D.999 |
在一个数列中,如果对任意 ,都有
,都有 为常数
为常数 ,那么这个数列叫做等积数列,
,那么这个数列叫做等积数列, 叫做这个数列的公积.已知数列
叫做这个数列的公积.已知数列 是等积数列,且
是等积数列,且 ,公积为
,公积为 ,记
,记 的前
的前 项和为
项和为 ,则:
,则:
(1) .
.
(2) .
.
在数列 中,对于任意
中,对于任意 ,若存在常数
,若存在常数 ,使得
,使得

 恒成立,则称数列
恒成立,则称数列 为
为 阶数列。现给出下列三个结论:
阶数列。现给出下列三个结论:
①若 ,则数列
,则数列 为1阶数列;
为1阶数列;
②若 ,则数列
,则数列 为2数列;
为2数列;
③若 ,则数列
,则数列 为3数列;以上结论正确的序号是
为3数列;以上结论正确的序号是
| A.①② | B.①③ | C.②③ | D.①②③ |
设 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
 .
.
(1)求满足“对任意的 ,
, ,都有
,都有 ”的有序数组(
”的有序数组( )的个数
)的个数 ;
;
(2)若对任意的 ,
, ,
, ,都有
,都有 成立,求满足“存在
成立,求满足“存在 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数
对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项与偶数项各有什么特点?并加以说明.
我们已经学过了等差数列,你是否想到过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项与偶数项各有什么特点?并加以说明.
对于各项均为整数的数列 ,如果
,如果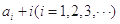 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:①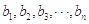 是
是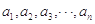 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列:
①数列1,2,3,4,5; ②数列1,2,3, ,11,12; ③数列 的前n项和为
的前n项和为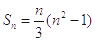 .
.
其中具有“P性质”或“变换P性质”的有( )
| A.③ | B.①③ | C.①② | D.①②③ |
如果数列 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意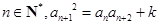 都成立,则称这样的数列
都成立,则称这样的数列 为“类等比数列” .由此等比数列必定是“类等比数列” .问:
为“类等比数列” .由此等比数列必定是“类等比数列” .问:
(1)各项均不为0的等差数列 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.
(2)若数列 为“类等比数列”,且
为“类等比数列”,且 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例.
(3)若数列 为“类等比数列”,且
为“类等比数列”,且 ,
, (a,b为常数),求数列
(a,b为常数),求数列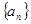 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
.
若数列 满足
满足 且
且 (其中
(其中 为常数),
为常数), 是数列
是数列 的前
的前 项和,数列
项和,数列 满足
满足 .
.
(1)求 的值;
的值;
(2)试判断 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求 (用
(用 表示).
表示).
数列 的前n项和为
的前n项和为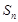 ,
, ,且对任意的
,且对任意的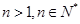 均满足
均满足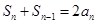 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
,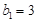 ,
,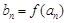 (
( ),求数列
),求数列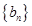 的前
的前 项和
项和 .
.
已知数列 满足
满足 ,给出下列命题:
,给出下列命题:
①当 时,数列
时,数列 为递减数列
为递减数列
②当 时,数列
时,数列 不一定有最大项
不一定有最大项
③当 时,数列
时,数列 为递减数列
为递减数列
④当 为正整数时,数列
为正整数时,数列 必有两项相等的最大项
必有两项相等的最大项
请写出正确的命题的序号____