对于一个有限数列
，定义
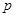的蔡查罗和（蔡查罗是一位数学家）为
，其中
．若一个99项的数列（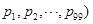
的蔡查罗和为1000，那么100项数列
的蔡查罗和为（ ）
| A．993 | B．995 | C．997 | D．999 |
，且
，
，则
的值等于（）
的最小值为3，则实数b的值为（）
为两个不重合的平面，下列命题中为真命题的是（）
则
则
则
则
” 的条件是“
”（）
等于（）
相关知识点
推荐套卷
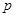对于一个有限数列，定义的蔡查罗和（蔡查罗是一位数学家）为，其中．若一个99项的数列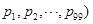（的蔡查罗和为1000，那么100项数列的蔡查罗和为（ ）
| A．993 | B．995 | C．997 | D．999 |
粤公网安备 44130202000953号