吉林省长春市高三第四次调研测试理科数学试卷
已知三条不重合的直线 和两个不重合的平面
和两个不重合的平面 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,且 ,且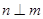 ,则 ,则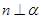 |
C.若 , ,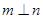 ,则 ,则 |
D.若 , , ,且 ,且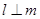 ,则 ,则 |
设变量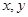 满足
满足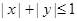 ,则
,则 的最大值和最小值分别为( )
的最大值和最小值分别为( )
| A.1,-1 | B.2,-2 | C.1,-2 | D.2,-1 |
按照下图的程序图计算,若开始输入的值为3,则最后输出的结果是( )
| A.6 | B.21 | C.5050 | D.231 |
某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则 的值为( )
的值为( )
| A.9 | B.10 | C.11 | D.13 |
曲线 在点
在点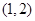 处的切线为
处的切线为 ,则直线
,则直线 上的任意点P与圆
上的任意点P与圆 上的任意点Q之间的最近距离是( )
上的任意点Q之间的最近距离是( )
A.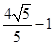 |
B.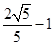 |
C. |
D.2 |
双曲线 的左、右焦点分别是
的左、右焦点分别是 ,过
,过 作倾斜角为
作倾斜角为 的直线交双曲线右支于点M,若
的直线交双曲线右支于点M,若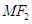 垂直于x轴,则双曲线的离心率为( )
垂直于x轴,则双曲线的离心率为( )
A.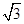 |
B.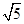 |
C.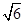 |
D. |
将一张边长为12cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置. 若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( )

A. |
B.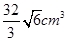 |
C.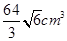 |
D.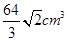 |
商场经营的某种袋装大米质量(单位:kg)服从正态分布 ,任取一袋大米,质量不足9.8kg的概率为 .(精确到0.0001)
,任取一袋大米,质量不足9.8kg的概率为 .(精确到0.0001)
将函数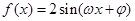
 的图形向右平移
的图形向右平移 个单位后得到
个单位后得到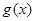 的图像,已知
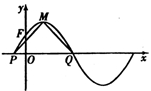
的图像,已知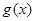 的部分图像如图所示,该图像与y轴相交于点
的部分图像如图所示,该图像与y轴相交于点 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且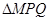 的面积为
的面积为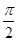 .
.
(1)求函数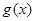 的解析式;
的解析式;
(2)在 中,
中, 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且 ,求
,求 面积的最大值.
面积的最大值.
由某种设备的使用年限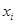 (年)与所支出的维修费
(年)与所支出的维修费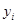 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果, ,
, ,
, ,
,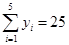 .
.
(1)求所支出的维修费y对使用年限x的线性回归方程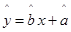 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程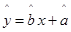 中,)
中,)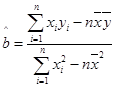 ,
, ,其中
,其中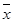 ,
,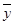 为样本平均值.)
为样本平均值.)
如图,在四棱柱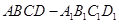 中,底面ABCD和侧面
中,底面ABCD和侧面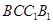 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,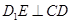 ,
,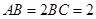 .
.
(1)求证: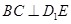 ;
;
(2)若平面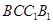 与平面
与平面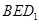 所成的锐二面角的大小为
所成的锐二面角的大小为 ,求线段
,求线段 的长度.
的长度.
如图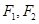 为椭圆C:
为椭圆C:
 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率 ,
,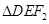 的面积为
的面积为 .若点
.若点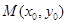 在椭圆C上,则点
在椭圆C上,则点 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线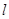 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.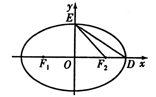
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点 的直线
的直线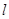 ,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
如图,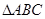 是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,
是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,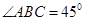 ,PD=1,DB=8.
,PD=1,DB=8.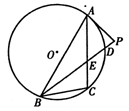
(1)求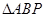 的面积;
的面积;
(2)求弦AC的长.
长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动,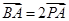 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)以直线AB的倾斜角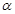 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;
(2)求点P到点D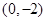 距离的最大值.
距离的最大值.
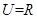 ,
, ,
,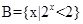 ,则图中阴影部分表示的集合为( )
,则图中阴影部分表示的集合为( )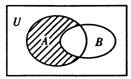
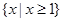



 对应的向量分别是
对应的向量分别是 ,则
,则 ( )
( )


 ,
,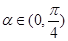 ,则
,则 ( )
( )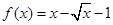 ,
,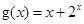 ,
, 的零点分别为
的零点分别为 ,则( )
,则( )
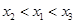
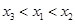

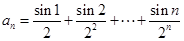 ,则对任意正整数
,则对任意正整数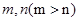 都成立的是( )
都成立的是( )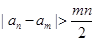

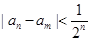
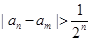
 ,
, ,若
,若 ,
, 在非零向量
在非零向量 上的投影相等,且
上的投影相等,且 ,则向量
,则向量 ,经计算得
,经计算得 ,
, ,
, ,
,
 ,观察上述结果,可归纳出的一般结论为 .
,观察上述结果,可归纳出的一般结论为 . 的4个实数根构成以q为公比的等比数列,若
的4个实数根构成以q为公比的等比数列,若 ,则
,则 的取值范围是 .
的取值范围是 .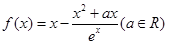 .
.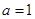 时,证明:当
时,证明:当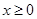 时,
时,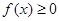 ;
;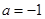 时,证明:
时,证明: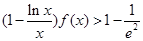 .
. ,且
,且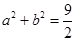 ,若
,若 恒成立.
恒成立. 对任意的
对任意的 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号