高中数学一阶、二阶线性常系数递归数列的通项公式试题

设关于x的不等式x²－x＜2nx(n∈N^*)的解集中整数的个数为a_n，数列{a_n}的前n项和为S_n，则的值为________．

已知数列{a_n}满足：a₁＝，a_n＋1＝ (n∈N^*)．
(1)求a₂，a₃的值；
(2)证明：不等式0＜a_n＜a_n＋1对于任意n∈N^*都成立．

若数列{a_n}满足＝d(n∈N^*，d为常数)，则称数列{a_n}为“调和数列”．已知正项数列为“调和数列”，且b₁＋b₂＋…＋b₉＝90，则b₄·b₆的最大值是(　　)．

A．10

B．100

C．200

D．400

已知数列{a_n}满足a_n＋1＝＋，且a₁＝，则该数列的前2 013项的和等于(　　)．

A．

B．3019

C．1508

D．013

设{a_n}是公比大于1的等比数列，S_n为数列{a_n}的前n项和．已知S₃＝7，且a₁＋3,3a₂，a₃＋4构成等差数列．
(1)求数列{a_n}的通项公式；
(2)令b_n＝ln a_3n＋1，n＝1,2，…，求数列{b_n}的前n项和T_n.

设{a_n}是公比不为1的等比数列，其前n项和为S_n，且a₅，a₃，a₄成等差数列．
(1)求数列{a_n}的公比；
(2)证明：对任意k∈N^*，S_k＋2，S_k，S_k＋1成等差数列．

已知数列{a_n}的前n项和为S_n，且满足S_n＝n²，数列{b_n}满足b_n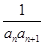＝，T_n为数列{b_n}的前n项和．
(1)求数列{a_n}的通项公式a_n和T_n；
(2)若对任意的n∈N^*，不等式λT_n<n＋(－1)ⁿ恒成立，求实数λ的取值范围．

已知数列{a_n}的通项公式是a_n＝－n²＋12n－32，其前n项和是S_n，对任意的m，n∈N^*且m<n，则S_n－S_m的最大值是(　　)．

A．－21

B．4

C．8

D．10

正项数列{a_n}的前n项和S_n满足：－(n²＋n－1)S_n－(n²＋n)＝0.
(1)求数列{a_n}的通项公式a_n；
(2)令b_n＝，数列{b_n}的前n项和为T_n，证明：对于任意的n∈N^*，都有T_n<.

设S_n为数列{a_n}的前n项和，若 (n∈N^*)是非零常数，则称该数列为“和等比数列”；若数列{c_n}是首项为2，公差为d(d≠0)的等差数列，且数列{c_n}是“和等比数列”，则d＝________.

在正项数列{a_n}中，a₁＝2，a_n＋1＝2a_n＋3×5ⁿ，则数列{a_n}的通项公式为________．

（本小题12分）已知函数．
(1)证明函数的图像关于点对称;
（2）若，求；
（3）在（2）的条件下，若 ，为数列的前项和，若对一切都成立，试求实数的取值范围．

已知函数f（x）=x²－ax+b（a，b∈R）的图像经过坐标原点，且，数列{}的前n项和=f（n）（n∈N^*）.
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若数列{}满足+ = ,求数列{}的前n项和.

随着科学技术的不断发展，人类通过计算机已找到了630万位的最大质数。陈成在学习中发现由41，43，47，53，61，71，83，97组成的数列中每一个数都是质数，他根据这列数的一个通项公式，得出了数列的后几项，发现它们也是质数。于是他断言：根据这个通项公式写出的数均为质数。请你写出这个通项公式                     ，从这个通项公式举出一个反例，说明陈成的说法是错误的：                            .

设数列的前n项积为；数列的前n项和为．
（1）设．①证明数列成等差数列；②求证数列的通项公式；
（2）若恒成立，求实数k的取值范围．