在数列 中,若
中,若
 ,则称
,则称 为“等方差数列”,下列是对“等方差数列”的判断;
为“等方差数列”,下列是对“等方差数列”的判断;
①若 是等方差数列,则
是等方差数列,则 是等差数列;
是等差数列;
② 是等方差数列;
是等方差数列;
③若 是等方差数列,则
是等方差数列,则 也是等方差数列;
也是等方差数列;
④若 既是等方差数列,又是等差数列,则该数列为常数列.
既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题序号为 ( )
| A.①②③ | B.①②④ | C.①②③④ | D.②③④ |
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为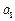 、公差为
、公差为

 的无穷等差数列.
的无穷等差数列.
(1)若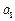 ,
, ,
, 成等比数列,求其公比
成等比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设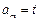 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 的无穷等比子数列.
的无穷等比子数列.
(本题满分18分;第(1)小题5分,第(2)小题5分,第(3)小题8分)
设数列 是等差数列,且公差为
是等差数列,且公差为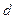 ,若数列
,若数列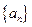 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若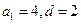 ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”;
(2)试判断数列 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么?
(3)设 是数列
是数列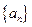 的前
的前 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使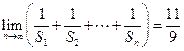 ;若存在,求
;若存在,求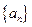 的通项公式,若不存在,说明理由.
的通项公式,若不存在,说明理由.
(本小题满分12分)
设数列 为等差数列,且
为等差数列,且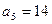 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
,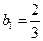 且
且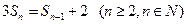 ;,
;,
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若 ,
, 为数列
为数列 的前
的前 项和. 求证:
项和. 求证: .
.
(本小题满分13分)
对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列 具有“
具有“ 性质”。
性质”。
不论数列 是否
是否 具有“
具有“ 性质”,如果存在与
性质”,如果存在与 不是同一数列的
不是同一数列的 ,且
,且 同
同
时满足下面两个条件:① 是
是 的一个排列
的一个排列 ;②数列
;②数列 具有“
具有“ 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换 性质”。
性质”。
(I)设数列 的前
的前 项和
项和 ,证明数列
,证明数列 具有“
具有“ 性质”;
性质”;
(II)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列 ,不具此性质的说明理由;
,不具此性质的说明理由;
(III)对于有限项数列 :1,2,3,…,
:1,2,3,…, ,某人已经验证当
,某人已经验证当 时,
时,
数列 具有“变换
具有“变换 性质”,试证明:当”
性质”,试证明:当” 时,数
时,数 列
列 也具有“变换
也具有“变换 性质”。
性质”。
已知点集 ,其中
,其中 ,
, ,点列
,点列 在L中,
在L中, 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列 的公差为1,
的公差为1, 。
。
(1)求数列 的通项公式;
的通项公式;
(2)若 =
= ,令
,令 ;试用解析式写出
;试用解析式写出 关于
关于 的函数。
的函数。
(3)若 =
= ,给定常数m(
,给定常数m( ),是否存在
),是否存在 ,使得
,使得 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。