已知点集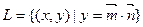 ,其中
,其中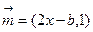 ,
, ,点列
,点列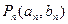 在L中,
在L中,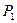 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列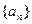 的公差为1,
的公差为1,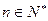 。
。
(1)求数列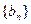 的通项公式;
的通项公式;
(2)若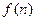 =
= ,令
,令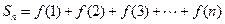 ;试用解析式写出
;试用解析式写出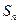 关于
关于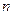 的函数。
的函数。
(3)若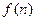 =
= ,给定常数m(
,给定常数m(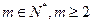 ),是否存在
),是否存在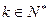 ,使得
,使得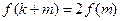 ,若存在,求出
,若存在,求出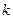 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
相关知识点
推荐套卷
已知点集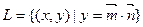 ,其中
,其中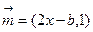 ,
, ,点列
,点列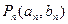 在L中,
在L中,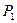 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列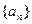 的公差为1,
的公差为1,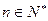 。
。
(1)求数列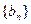 的通项公式;
的通项公式;
(2)若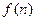 =
= ,令
,令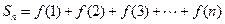 ;试用解析式写出
;试用解析式写出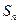 关于
关于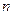 的函数。
的函数。
(3)若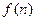 =
= ,给定常数m(
,给定常数m(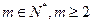 ),是否存在
),是否存在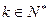 ,使得
,使得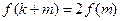 ,若存在,求出
,若存在,求出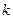 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。