高中数学一阶、二阶线性常系数递归数列的通项公式试题

已知数列{a_n}的通项公式是a_n=2n-3()ⁿ,则其前20项和为(　　)

A．380-(1-)	B．400-(1-)
C．420-(1-)	D．440-(1-)

已知{a_n}是各项均为正数的等比数列,且a₁+a₂=2(+),a₃+a₄+a₅=64(++),
(1)求{a_n}的通项公式.
(2)设b_n=(a_n+)²,求数列{b_n}的前n项和T_n.

已知二次函数f(x)=px²+qx(p≠0),其导函数为f'(x)=6x-2,数列{a_n}的前n项和为S_n,点(n,S_n)(n∈N^*)均在函数y=f(x)的图象上.
(1)求数列{a_n}的通项公式.
(2)若c_n=(a_n+2),2b₁+2²b₂+2³b₃+…+2ⁿb_n=c_n,求数列{b_n}的通项公式.

定义:F(x,y)=y^x(x>0,y>0),已知数列{a_n}满足:a_n=(n∈N^*),若对任意正整数n,都有a_n≥a_k(k∈N^*)成立,则a_k的值为(　　)

A．

B．2

C．3

D．4

设两数列{a_n}和{b_n}，a_n＝，b_n＝，则数列的前n项的和为(　　)

A．	B．
C．	D．

已知数列{a_n}，如果数列{b_n}满足b₁＝a₁，b_n＝a_n＋a_n－1，n≥2，n∈N^*，则称数列{b_n}是数列{a_n}的“生成数列”．
(1)若数列{a_n}的通项为a_n＝n，写出数列{a_n}的“生成数列”{b_n}的通项公式；
(2)若数列{c_n}的通项为c_n＝2n＋b(其中b是常数)，试问数列{c_n}的“生成数列”{q_n}是否是等差数列，请说明理由；
(3)已知数列{d_n}的通项为d_n＝2ⁿ＋n，求数列{d_n}的“生成数列”{p_n}的前n项和T_n.

设正项数列{a_n}的前n项和为S_n，若{a_n}和{}都是等差数列，且公差相等．
(1)求{a_n}的通项公式；
(2)若a₁，a₂，a₅恰为等比数列{b_n}的前三项，记数列c_n＝，数列{c_n}的前n项和为T_n.求证：对任意n∈N^*，都有T_n<2.

已知向量p＝(a_n,2ⁿ)，向量q＝(2^n＋1，－a_n＋1)，n∈N^*，向量p与q垂直，且a₁＝1.
(1)求数列{a_n}的通项公式；
(2)若数列{b_n}满足b_n＝log₂a_n＋1，求数列{a_n·b_n}的前n项和S_n.

对于数列{a_n}，定义数列{a_n＋1－a_n}为数列{a_n}的“差数列”，若a₁＝2，{a_n}的“差数列”的通项为2ⁿ，则数列{a_n}的前n项和S_n＝________.

已知曲线C：y＝ (x>0)及两点A₁(x_1,0)和A₂(x_2,0)，其中x₂>x₁>0.过A₁，A₂分别作x轴的垂线，交曲线C于B₁，B₂两点，直线B₁B₂与x轴交于点A₃(x_3,0)，那么(　　)

A．x1，，x2成等差数列	B．x1，，x2成等比数列
C．x1，x3，x2成等差数列	D．x1，x3，x2成等比数列

已知数列{a_n}的前n项和为S_n，且满足S_n＝n²，数列{b_n}满足b_n＝，T_n为数列{b_n}的前n项和．
(1)求数列{a_n}的通项公式a_n和T_n；
(2)若对任意的n∈N^*，不等式λT_n<n＋(－1)ⁿ恒成立，求实数λ的取值范围．

已知等差数列{a_n}满足：a₂＝5，a₄＋a₆＝22，数列{b_n}满足b₁＋2b₂＋…＋2^n－1b_n＝na_n，设数列{b_n}的前n项和为S_n.
(1)求数列{a_n}，{b_n}的通项公式；
(2)求满足13<S_n<14的n的集合．

已知数列{a_n}的前n项和是S_n，且S_n＋a_n＝1.
(1)求数列{a_n}的通项公式；
(2)记b_n＝log₃，数列的前n项和为T_n，证明：T_n<.

已知数列的前n项和
（1）求数列的通项公式,并证明是等差数列；
（2）若，求数列的前项和

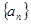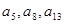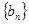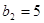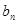数列是公差不为零的等差数列，并且是等比数列的相邻三项，若，则等于（   ）

A．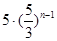

B．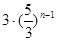

C．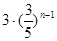

D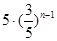．