已知数列{an},如果数列{bn}满足b1=a1,bn=an+an-1,n≥2,n∈N*,则称数列{bn}是数列{an}的“生成数列”.
(1)若数列{an}的通项为an=n,写出数列{an}的“生成数列”{bn}的通项公式;
(2)若数列{cn}的通项为cn=2n+b(其中b是常数),试问数列{cn}的“生成数列”{qn}是否是等差数列,请说明理由;
(3)已知数列{dn}的通项为dn=2n+n,求数列{dn}的“生成数列”{pn}的前n项和Tn.
相关知识点
推荐套卷
 中,
中,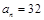 ,
, ,
,
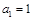 为首项的等比数列,求数列
为首项的等比数列,求数列 的前m项和
的前m项和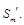
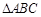 中,角
中,角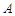 、
、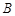 、
、 的对边分别为
的对边分别为 、
、 、
、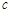 ,
, ,
,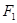 、
、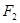 分别为椭圆
分别为椭圆 :
: 的上、下焦点,其中
的上、下焦点,其中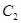 :
:  的焦点,点
的焦点,点 是
是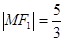 。
。
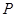 (1,3)和圆
(1,3)和圆 :
: ,过点
,过点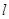 与圆
与圆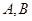 ,在线段
,在线段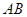 取一点
取一点 ,满足:
,满足: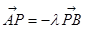 ,
,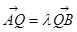 (
( 且
且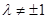 )。
)。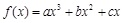 (
(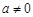 )是定义在
)是定义在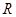 上的奇函数,且
上的奇函数,且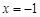 时,函数
时,函数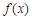 取极值1.
取极值1.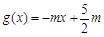 ,若
,若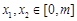 (
(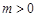 ),不等式
),不等式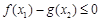 恒成立,求实数
恒成立,求实数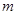 的取值范围;
的取值范围;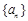 的前n项和为
的前n项和为 ,
,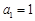 ,且
,且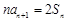 ,数列
,数列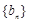 满足
满足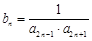 ,数列
,数列 的前n项和为
的前n项和为 (其中
(其中 ).
).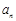 和
和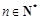 ,不等式
,不等式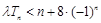 恒成立,求实数
恒成立,求实数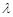 的取值范围
的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号