高中数学不定方程和方程组解答题

已知函数y=f（x）对任意的实数ab都有：f（a+b）=f（a）+f（b）﹣1，且x＞0时，f（x）＞1，
（1）求证：f（x）是R上的增函数；
（2）若f（4）=5，求f（2）的值，并解不等式f（3m²﹣m﹣2）＜3．

已知函数．
(1)求函数的单调区间，并指出其增减性；
(2)若关于x的方程至少有三个不相等的实数根，求实数a的取值范围．

已知函数．
（1）当时，求函数的零点；
（2）若函数有零点，求实数的取值范围．

已知定义在上的函数满足，当时，，且．
（Ⅰ）求的值；
（Ⅱ）当时，关于的方程有解，求的取值范围．

（本小题满分12分）设函数的导函数为，若函数的图像关于直线对称，且.
（1）求实数a、b的值
（2）若函数恰有三个零点，求实数的取值范围。

（本小题满分12分）已知二次函数对任意实数都满足，且．令．
（1）若函数在上的最小值为0，求的值；
（2）记函数，若函数有5个不同的零点，求实数的取值范围．

已知函数是定义在上的奇函数．当时，，且图象过点与点.
（Ⅰ）求实数的值，并求函数的解析式；
（Ⅱ）若关于的方程有两个不同的实数解，请写出实数的取值范围；
（Ⅲ）解关于的不等式，写出解集.

（本小题12分）已知函数
（1）当时，求方程的解；
（2）若方程在上有实数根，求实数的取值范围；
（3）当时，若对任意的，总存在，使成立，求实数的取值范围．

已知函数，．
（1）若函数在点处的切线方程为，求的值；
（2）若函数有三个不同的极值点，求的值；
（3）若存在实数，使对任意的，不等式恒成立，求正整数的最大值．

【原创】设命题p：直线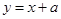与圆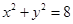有公共点，命题q:关于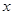的方程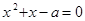的一根大于1，另一根小于1，命题“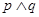”为假命题，命题“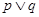”为真命题，求实数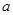的取值范围．

（本小题满分12分）设函数（其中为自然对数的底数，，），曲线在点处的切线方程为．
（1）求的值；
（2）若对任意，函数有且只有两个零点，求的取值范围．

某校高一（1）班共有学生50人，据统计原来每人每年用于购买饮料的平均支出是a元．经测算和市场调查，若该班学生
集体改饮某品牌的桶装纯净水，则年总费用由两部分组
成，一部分是购买纯净水的费用，另一部分是其它费用
780元，其中，纯净水的销售价x(元/桶)与年购买总量
y (桶)之间满足如图所示关系．
（1）求y与x的函数关系式；
（2）若该班每年需要纯净水380桶，且a 为120时，
请你根据提供的信息分析一下：该班学生集体改饮桶装
纯净水与个人买饮料，哪一种花钱更少？
（3）当a至少为多少时, 该班学生集体改饮桶装纯净
水一定合算？从计算结果看，你有何感想（不超过30字）？

（本小题满分12分）若、是关于的二次方程的两根， 
且，求的范围。

已知函数．
（1）当时，求的单调减区间；
（2）若方程恰好有一个正根和一个负根，求实数的最大值．

（本小题12分）已知函数．
（Ⅰ）若是偶函数，求实数m的值；
（Ⅱ）当时，关于x的方程在区间上恰有两个不同的实数解，求m的范围．