高中数学不定方程和方程组解答题

（本小题共12分）已知函数（为自然对数的底），（为常数），是实数集R上的奇函数．
（1）求证：；
（2）讨论关于的方程：的根的个数．

设函数f（x） =-6x+5，．
（1）求f（x）的极值；
（2）若关于x的方程 f（x） = a有3个不同实根，求实数a的取值范围；
（3）已知当．时，f（x） 恒成立，求实数 k的取值范围

已知函数，
（1）对任意的，成立，求的取值范围；
（2）对，有两个不等实根，求的取值范围．

已知函数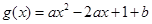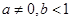（），在区间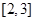上有最大值4，最小值1，设．
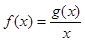（1）求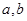的值；
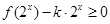（2）不等式在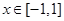上恒成立，求实数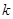的取值范围；
（3）方程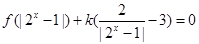有三个不同的实数解，求实数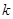的取值范围．

已知函数．
（1）当时，证明函数只有一个零点；
（2）若函数在区间上是减函数，求实数的取值范围．

设函数
（1）画出的简图；
（2）若方程有三个不等实根，求k值的集合；
（3）如果时，函数的图象总在直线的下方，试求出k值的集合。

若下列方程：x＋4ax－4a＋3＝0， x＋(a－1)x＋a＝0, x＋2ax－2a＝0至少有一个方程有实根。试求实数a的取值范围。

设函数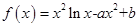在点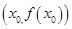处的切线方程为.
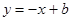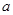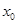(1)求实数及的值；
(2)求证：对任意实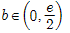数，函数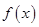有且仅有两个零点.

4-5：不等式选讲（本小题满分10分）
已知函数．
（1）若是定义域为的奇函数，试求实数的值；
（2）在（1）的条件下，若函数有三个零点，试求实数的取值范围．

已知函数是偶函数．
（Ⅰ）求的值；
（Ⅱ）设,若函数与的图象有且只有一个公共点，求实数的取值范围．

（本小题满分14分）
已知函数（），且.
（1）求α的值；
（2）求函数的零点；
（3）判断在（-∞，0）上的单调性，并给予证明．

某投资公司计划投资A，B两种金融产品，根据市场调查与预测，A产品的利润与投资量成正比，其关系如图1，B产品的利润与投资量的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）

（1）分别将A，B两产品的利润表示为投资量的函数关系式；
（2）该公司已有10万元资金，并全部投入A，B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？

(1)m为何值时，f(x)＝x²＋2mx＋3m＋4.
①有且仅有一个零点；②有两个零点且均比－1大；
(2)若函数f(x)＝|4x－x²|＋a有4个零点，求实数a的取值范围．

设命题：方程无实数根；命题：函数的定义域是．如果命题为真命题，求实数的取值范围．

已知函数，．
（1） 求的最小值（用表示）；     
（2） 关于的方程有解，求实数的取值范围．