广东省肇庆市高一上学期期末考试数学试卷
已知集合M={-1,0,1},N={0,1,2},则M∪N=
| A.{-1,0,1,2} | B.{-1,0,1} | C.{-1,0,2} | D.{0,1} |
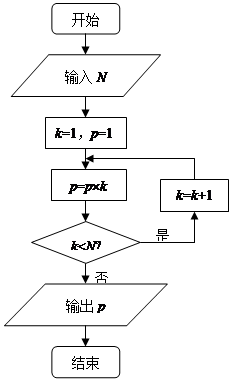
为了解2000名学生对学校食堂的意见,准备从中抽取一个样本容量为50的样本. 若采用系统抽样,则分段间隔k为
| A.20 | B.30 | C.40 | D.50 |
已知一组数据为0,3,5,x,9,13,且这组数据的中位数为7,那么这组数据的众数为
| A.13 | B.9 | C.7 | D.0 |
已知曲线 与
与 的交点的横坐标是
的交点的横坐标是 ,则
,则 的取值范围是
的取值范围是
A.(0,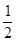 ) ) |
B.{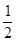 } } |
C.(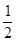 ,1) ,1) |
D.(1,2) |
已知函数 ,若
,若 ,则x的取值范围是
,则x的取值范围是
| A.(-∞,-1) ∪(1,+∞) | B.(-1,0)∪(0,1) |
| C.(-∞,-1) ∪(0,1) | D.(-1,0)∪(1,+∞) |
将容量为n的样本中的数据分成6组,绘制频率分布直方图. 若第一组至第六组数据的频率之比为2:3:4:6: 4:1,且前三组数据的频数之和等于36,则n等于 .
(本小题满分12分)
A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
 |
80 |
75 |
70 |
65 |
60 |
 |
70 |
66 |
68 |
64 |
62 |
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(参考数值:  ,
, )
)
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(结果保留整数).
(本小题满分12分)
已知函数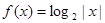 .
.
(1)求函数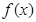 的定义域及
的定义域及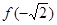 的值;
的值;
(2)判断函数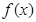 的奇偶性;
的奇偶性;
(3)判断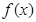 在(0,+∞)上的单调性,并给予证明.
在(0,+∞)上的单调性,并给予证明.
(本小题满分14分)
某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示. 质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
| 车间 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
(本小题满分14分)
已知函数 (
( ),且
),且 .
.
(1)求α的值;
(2)求函数 的零点;
的零点;
(3)判断 在(-∞,0)上的单调性,并给予证明.
在(-∞,0)上的单调性,并给予证明.
(本小题满分14分)
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台. 现销售给A地10台,B地8台. 已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的费用分别为300元和500元.
(1)设从甲地调运x台至A地,求总费用y关于台数x的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.
 ,
, ,则
,则
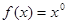 与
与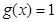
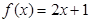 与
与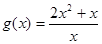
 与
与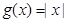
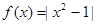 与
与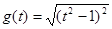

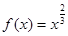

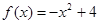
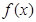 (
(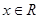 )为奇函数,
)为奇函数, ,
, ,则
,则

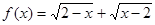 的定义域是 .
的定义域是 . 在
在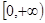 上单调递减,且
上单调递减,且 . 若
. 若 ,则x的取值范围是 .
,则x的取值范围是 .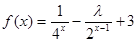 (
(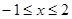 ).
).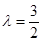 时,求函数
时,求函数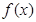 的值域;
的值域; 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号