某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
已知函数 .
.
(1)当 时,求
时,求 的单调减区间;
的单调减区间;
(2)若方程 恰好有一个正根和一个负根,求实数
恰好有一个正根和一个负根,求实数 的最大值.
的最大值.
(本题12分)已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p或q”是假命题,求a的取值范围.
(本小题满分14分) 设函数
设函数 ,且
,且 ,
, .求证:
.求证: (Ⅰ)
(Ⅰ) 且
且 ;
; (Ⅱ)方程
(Ⅱ)方程 在区间
在区间 内至少有一个根;
内至少有一个根; (Ⅲ)设
(Ⅲ)设 ,
, 是方程
是方程 的两个根,则
的两个根,则 .
.


(12分)已知函数 在区间[-1,1]上与x轴有且只有一个交点,求:实数
在区间[-1,1]上与x轴有且只有一个交点,求:实数 的取值范围。
的取值范围。
已知函数 且
且 .
.
(Ⅰ) 若1是关于x的方程 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当 且
且 时,解不等式
时,解不等式 ;
;
(Ⅲ)若函数 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
(本小题满分14分)已知 为常数,且
为常数,且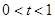 ,函数
,函数 的最小值和函数
的最小值和函数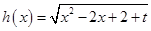 的最小值都是函数
的最小值都是函数
 R
R 的零点.
的零点.
(1)用含 的式子表示
的式子表示 ,并求出
,并求出 的取值范围;
的取值范围;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.