高中数学不定方程和方程组解答题

（本小题满分14分）已知命题：方程有两个不相等的实根；命题：关于的不等式对任意的实数恒成立．若“”为真，“”为假，求实数的取值范围．

（本小题满分12分）已知定义域为的函数满足
（1）若，求；又若，求；
（2）设有且仅有一个实数，使得，求函数的解析式．

（本小题满分14分）已知  
（1）求，；  
（2）画出的图像；
（3）若，问为何值时,方程没有根？有一个根？两个根？

已知函数
（1）若方程有两不相等的正根，求的取值范围；
（2）求在的最小值.

（本小题满分10分）解下列的方程、方程组及不等式组：
（1）；       
（2）

（本小题满分12分）已知函数是定义域为的偶函数，当时，．
（Ⅰ）在给定的图示中画出函数的图象（不需列表）；

（Ⅱ）求函数的解析式；
（Ⅲ）若方程有两解，求的范围.（只需写出结果，不要解答过程)

设函数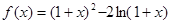
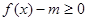（1）若关于的不等式在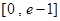有实数解，求实数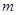的取值范围；    
（2）设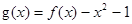，若关于的方程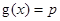至少有一个解，求 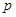的最小值．  
（3）证明不等式：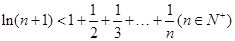    

设函数
（1）讨论的单调性；
（2）当时，函数的图像有三个不同的交点，求实数m的范围．

已知
（1）求的极值点；
（2）当时，若方程在上有两个实数解，求实数t的取值范围；
（3）证明：当时，。

已知向量，，且是方程的两个实根．
（1）求实数的取值范围；
（2）设，求的最小值．

（本小题满分12分，（Ⅰ）小问2分，（Ⅱ）小问3分，（Ⅲ）小问5分）
已知a，b，c，d是不全为零的实数，函数，，方程
的实根都是的实根；反之，方程的实根都是的实根．
（Ⅰ）求d的值；
（Ⅱ）若，求c的取值范围；
（Ⅲ）若，，求c的取值范围．

已知函数．
（1）当，且是上的增函数，求实数的取值范围；
（2）当，且对任意实数，关于的方程总有三个不相等的实数根，求实数的取值范围．

已知为奇函数，为偶函数，且．
（1）求函数及的解析式；
（2）用函数单调性的定义证明：函数在上是减函数；
（3）若关于的方程有解，求实数的取值范围．

已知定义在区间上的函数，其中常数．
（1）若函数分别在区间上单调，试求的取值范围；
（2）当时，方程有四个不相等的实根．
①证明：；
②是否存在实数，使得函数在区间单调，且的取值范围为，若存在，求出的取值范围；若不存在，请说明理由．

已知命题P：“，都有不等式成立”，命题Q：“关于的方程只有一个实数根”
（Ⅰ）若命题P是真命题，求实数的取值集合B；
（Ⅱ）若命题“P且Q”为假，命题“P或Q”为真，求实数的取值范围．