高中数学不定方程和方程组解答题

已知函数．
（1）若函数在区间[-1，1]上存在零点，求实数a的取值范围；
（2）当a=0时，若对任意的，总存在，使成立，求实数m的取值范围．

已知一次函数满足．
（1）求这个函数的解析式；
（2）若函数，求函数的零点．

定义在（0，＋∞）上的函数f（x），对于任意的m，n∈（0，＋∞），都有f（mn）＝f（m）＋f（n）成立，当x＞1时，f（x）＜0．
（1）求证：1是函数f（x）的零点；
（2）求证：f（x）是（0，＋∞）上的减函数；
（3）当f （2）＝  时，解不等式f （ax＋4）＞1．

给定两个命题: P：对任意实数都有恒成立；Q：关于的方程有实数根；如果P与Q中有且仅有一个为真命题，求实数的取值范围．

（本小题满分12分）已知是定义在上的偶函数，且当时，．
（1）求的解析式；
（2）在所给的坐标系内画出函数的草图，并求方程恰有两个不同实根时的实数的取值范围．

已知函数

（1）若a＝1，求函数f（x）的零点；
（2）若函数f（x）在[－1，＋∞）上为增函数，求a的取值范围．

已知．（1）求函数的单调区间；
（2）若关于的方程有实数解,求实数的取值范围；
（3）当时,求证：．

设函数，且，函数．
（1）求的解析式；
（2）若方程－b=0在 [－2，2]上有两个不同的解，求实数b的取值范围．

已知函数
（1）若函数在上无零点，请你探究函数在上的单调性；
（2）设，若对任意的，恒有成立，求实数的取值范围．

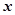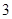（本小题满分12分）甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品（百台），其总成本为（万元），其中固定成本为万元，并且每生产1百台的生产成本为1万元（总成本固定成本+生产成本），销售收入，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，请完成下列问题
（1）写出利润函数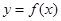的解析式（利润销售收入—总成本）；
（2）甲厂生产多少台新产品时，可使盈利最多？

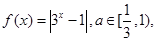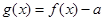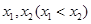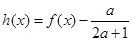已知函数若函数有两个不同的零点，函数有两个不同的零点．
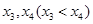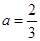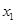（1）若，求的值；
（2）求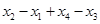的最小值．

（本题12分）已知是定义在R上的偶函数，当时，
（1）求的值；
（2）求的解析式并画出简图；      

（3）讨论方程的根的情况。

（本小题满分12分）
已知定义域为R的奇函数满足，且当时，．
（1）求在区间[－1，1]上的解析式．
（2）当m取何值时，方程在区间（0，1）上有解？

（本小题满分12分）已知二次函数对任意实数都满足，且．令．
（1）若函数在上的最小值为0，求的值；
（2）记函数，若函数有5个不同的零点，求实数的取值范围．

已知函数．
（1）当时，写出的单调区间；
（2）当时，求的最小值；
（3）试讨论关于的方程的解的个数．