高中数学不定方程和方程组解答题

已知函数
（1）若在区间上是增函数，求实数a的取值范围；
（2）若是的极值点，求在上的最大值；
（3）在（2）的条件下，是否存在实数，使得函数的图象与函数的图象恰有个交点，若存在，请求出实数的取值范围；若不存在，试说明理由.

已知函数f（x）=x+的定义域为（0，+∞），且f（2）=2+．设点P是函数图象上的任意一点，过点P分别作直线y=x和y轴的垂线，垂足分别为M、N．
（1）求a的值．
（2）问：|PM|•|PN|是否为定值？若是，则求出该定值；若不是，请说明理由．
（3）设O为坐标原点，求四边形OMPN面积的最小值．

设函数 $f\left(x\right)=x^3+2a{x}^2+bx+a,g\left(x\right)=x^2-3x+2$，其中 $x\in R$， $a,b$为常数，已知曲线 $y=f\left(x\right)$与 $y=g\left(x\right)$在点 $(2,0)$处有相同的切线 $l$．
（Ⅰ）求 $a,b$的值，并写出切线 $l$的方程；
（Ⅱ）若方程 $f\left(x\right)+g\left(x\right)=mx$有三个互不相同的实根 $0,x_1,x_2$，其中 $x_1<x_2$，且对任意的 $x\in [x_1,x_2],f\left(x\right)+g\left(x\right)<m(x-1)$恒成立，求实数 $m$的取值范围．

如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM＝PN＝MN＝2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远)．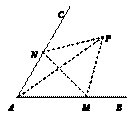

已知是二次函数，不等式的解集是(0，5)，且在区间[-1，4]上的最大值是12．
（1）求f(x)的解析式；
（2）是否存在正整数m,使得方程在区间内有且只有两个不等的实数根？若存在，求出所有m的值；若不存在，请说明理由．

已知函数，其中.
（1）若，求函数的定义域和极值；
（2）当时，试确定函数的零点个数，并证明.

某村庄拟修建一个无盖的圆柱形蓄水池（不计厚度）.设该蓄水池的底面半径为米，高为米，体积为立方米．假设建造成本仅与表面积有关，侧面积的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12000元（π为圆周率）．
（1）将表示成的函数，并求该函数的定义域；
（2）讨论函数的单调性，并确定和为何值时该蓄水池的体积最大．

某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为 $\frac{80\pi }{3}$立方米，且 $1\ge 2r$．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为 $c(c>3)$千元．设该容器的建造费用为 $y$千元．
（1）写出 $y$关于 $r$的函数表达式，并求该函数的定义域；
（2）求该容器的建造费用最小时的 $r$．

设函数中，为奇数，均为整数，且均为奇数.求证：无整数根。

设函数中，为奇数，均为整数，且均为奇数.求证：无整数根。

已知函数f(x)=2^x,g(x)=+2.
(1)求函数g(x)的值域.
(2)求满足方程f(x)-g(x)=0的x的值.

在△中，角所对的边分别为、、,若、是方程的两根，且;
（1）求角的大小；
（2）求边的长度；
（3）求的面积。

已知函数(a是常数，a∈R)
（1）当a=1时求不等式的解集．
（2）如果函数恰有两个不同的零点，求a的取值范围．

已知函数(a是常数，a∈R)
（1）当a=1时求不等式的解集．
（2）如果函数恰有两个不同的零点，求a的取值范围．

某幼儿园准备建一个转盘，转盘的外围是一个周长为k米的圆．在这个圆上安装座位，且每个座位和圆心处的支点都有一根直的钢管相连经预算，转盘上的每个座位与支点相连的钢管的费用为3k元/根，且当两相邻的座位之间的圆弧长为x米时，相邻两座位之间的钢管和其中一个座位的总费用为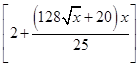k元．假设座位等距分布，且至少有两个座位，所有座位都视为点，且不考虑其他因素，记转盘的总造价为y元．
(1)试写出y关于x的函数关系式，并写出定义域；
(2)当k＝50米时，试确定座位的个数，使得总造价最低？