已知函数
(1) 若函数 的图象经过
的图象经过 (3,4)点,求
(3,4)点,求 的值;
的值;
(2) 若 ,求
,求 的值;
的值;
(3) 比较 大小,并写出比较过程.
大小,并写出比较过程.
(本题满分10分)
已知函数 (a、b是常数且a>0,a≠1)在区间[-
(a、b是常数且a>0,a≠1)在区间[-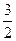 ,0]上有ymax=3,ymin=
,0]上有ymax=3,ymin= ,试求a和b的值.。
,试求a和b的值.。
(本小题满分15分)
已知函数 ,
, 。
。
(Ⅰ)求 在区间
在区间 的最小值;
的最小值;
(Ⅱ)求证:若 ,则不等式
,则不等式 ≥
≥ 对于任意的
对于任意的 恒成立;
恒成立;
(Ⅲ)求证:若 ,则不等式
,则不等式 ≥
≥ 对于任意
对于任意 的
的
 恒成立。
恒成立。
(本小题满分12分)
已知函数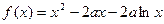 (
( ,
, ),
), .
.
(Ⅰ)证明:当 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数 、
、 ,均有
,均有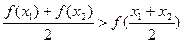 成立;
成立;
(Ⅱ)记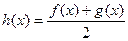 ,
,
(ⅰ)若 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(ⅱ)证明: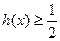 .
.
((本题15分)
已知点(1, )是函数
)是函数 且
且 )的图象上一点,等
)的图象上一点,等 比数列
比数列 的前n项和为
的前n项和为 ,数列
,数列
 的首项为c,且前n项和
的首项为c,且前n项和 满足
满足 -
- =
= +
+ (n
(n 2)
2)
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列{ 前n项和为
前n项和为 ,问
,问 >
> 的最小正整数n是多少?
的最小正整数n是多少?
、 已知 ≤
≤ ≤1,若函数
≤1,若函数 在区间[1,3]上的最大值为
在区间[1,3]上的最大值为 ,最小值为
,最小值为 ,令
,令 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断并证明函数 在区间[
在区间[ ,1]上的单调性;并求出
,1]上的单调性;并求出 的最小值 .
的最小值 .