命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.已知函数f(x)=1+a +
+ ,g(x)=
,g(x)=
 .
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[ ,3]上的所有上界构成的集合;
,3]上的所有上界构成的集合;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a•2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
已知函数f(x)=a|x+b|(a>0,a≠1,b∈R).
(1)若f(x)为偶函数,求b的值;
(2)若f(x)在区间[2,+∞)上是增函数,试求a、b应满足的条件.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数 的图象与直线
的图象与直线 没有交点,求b的取值范围;
没有交点,求b的取值范围;
(3)设 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求
的图象有且只有一个公共点,求 的取值范围.
的取值范围.
设f(x)=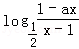 为奇函数,a为常数.
为奇函数,a为常数.
(1)求a的值;
(2)判断f(x)在区间(1,+∞)上的单调性,并证明你的结论;
(3)若对于区间(3,4)上的每一个x的值,不等式f(x)>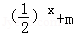 恒成立,
恒成立,
求实数m的取值范围.
(1)计算:(2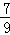 )
)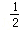 +(lg5)0+(
+(lg5)0+(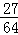 )
) ;
;
(2)解方程:log3(6x﹣9)=3.
已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,求g(x)的解析式.
(1)若xlog32=1,试求4x+4﹣x的值;
(2)计算:(2 )
) ﹣(﹣9.6)0﹣(3
﹣(﹣9.6)0﹣(3 )
) +(1.5)﹣2+(
+(1.5)﹣2+( ×
× )4.
)4.
已知函数f(x)=ax﹣1(a>0且a≠1)
(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较 与f(﹣2.1)大小,并写出比较过程.
与f(﹣2.1)大小,并写出比较过程.