高中数学原根与指数解答题

（本题11分）已知函数为奇函数．
（1）求实数的值；
（2）若关于的不等式只有一个整数解，求实数的取值范围．

命题p：关于x的不等式x²+2ax+4＞0，对一切x∈R恒成立，命题q：指数函数f（x）=（3﹣2a）^x是增函数，若p∨q为真，p∧q为假，求实数a的取值范围．

已知指数函数满足：，定义域为的函数是奇函数．
（1）确定和的解析式；
（2）判断函数的单调性，并用定义证明；
（3）若对于任意，都有成立，求的取值范围．

（本小题满分12分）已知函数．
（Ⅰ）若，求的值；
（Ⅱ）若对于任意实数恒成立，求实数的取值范围．

已知函数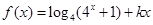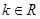（）是偶函数．
（1）求实数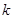的值；
（2）证明：对任意的实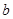数，函数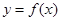的图象与直线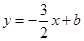最多只有一个公共点；
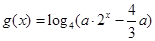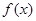（3）设，若与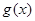的图象有且只有一个公共点，求实数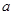的取值范围．

（本小题满分10分）已知函数 （a＞0,且a≠1），=．
（1）函数的图象恒过定点A，求A点坐标；
（2）若函数的图像过点（2,），证明：方程在（1，2）上有唯一解．

设f（x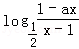）=为奇函数，a为常数．
（1）求a的值；
（2）判断f（x）在区间（1，+∞）上的单调性，并证明你的结论；
（3）若对于区间（3，4）上的每一个x的值，不等式f（x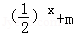）＞恒成立，
求实数m的取值范围．

（本小题满分12分）
已知函数的图象过点（0，-2），（2，0）
（1）求与的值;
（2）求时，的最大值与最小值．

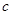已知函数（其中是常数）.
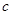（1）若当时，恒有成立，求实数的取值范围；
（2）若存在，使成立，求实数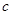的取值范围；
（3）若方程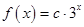在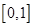上有唯一实数解，求实数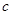的取值范围.

已知.
（I）判断的奇偶性；
（II）求的值域.

已知函数
（1）求；
（2）求的值；
（3）求

（本小题满分10分）已知函数（其中），﹒
（1）若命题“”是真命题，求x的取值范围；
（2）设命题p：，或，若是假命题，求m的取值范围﹒

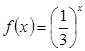已知函数，，函数的最小值为．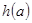
（1）求；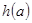
（2）是否存在实数、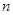同时满足以下条件：
①；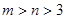
②当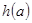的定义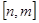域为时，值域为．若存在，求出、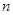的值；若不存在，说明理由

设．
（1）求的值；
（2）求的最小值．

已知函数的图象恒过定点，且点又在函数的图象上．
（1）求实数的值；               
（2）解不等式；
（3）函数的图象与直线有两个不同的交点时，求的取值范围．