(本题满分14分,第1小题满分4分,第2小题满分4分,第3小题满分6分)
设函数 ,
,
(1)求 的反函数
的反函数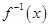 ;
;
(2)判断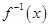 的单调性,不必证明;
的单调性,不必证明;
(3)令 ,当
,当

 ,
, 时,
时,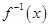 在
在 上的值域是
上的值域是 ,求
,求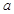 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求满足
时,求满足 的
的 的取值范围;
的取值范围;
(2)若 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 的解析式,判断其在R上的单调性并加以证明.
的解析式,判断其在R上的单调性并加以证明.
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
.(本小题满分12分)
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
(本小题满分12分)
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当a,b满足什么条件时,f(x)在(1,+∞)上恒取正值.
(本小题满分12分)
若函数 为奇函数,当
为奇函数,当 时,
时, (如图).
(如图).
(1)请补全函数 的图象;(2)写出函数
的图象;(2)写出函数 的表达式;
的表达式;
(3)用定义证明函数 在区间
在区间 上单调递增
上单调递增
已知函数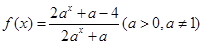 是定义在R上的奇函数.
是定义在R上的奇函数.
(I)求实数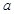 的值;
的值;
(II)判断 在定义域上的单调性,并用单调性定义证明;
在定义域上的单调性,并用单调性定义证明;
(III)当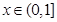 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程 有实数根;②函数
有实数根;②函数 ”
”
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(III)对于M中的函数 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 当
当 且
且