(本小题满分12分)
甲、乙两名射击运动员，甲射击一次命中10环的概率为
，乙射击一次命中10环的概率为s，若他们各自独立地射击两次，设乙命中10环的次数为ξ，且ξ的数学期望Eξ=
，
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及的分布列， (2)求的数学期望.
（本小题满分12分）
在一次篮球练习课中，规定每人最多投篮5次，若投中2次就称为“通过”，若投中3次就称为“优秀”并停止投篮．已知甲每次投篮投中的概率是
．
（I）求甲恰好投篮3次就通过的概率；
（II）设甲投篮投中的次数为
，求随机变量的分布列及数学期望E．
有混在一起质地均匀且粗细相同的长分别为1
、2、3的钢管各3根（每根钢管附有不同的编号），现随意抽取4根（假设各钢管被抽取的可能性是均等的），再将抽取的4根首尾相接焊成笔直的一根．
（1）若用ξ表示新焊成的钢管的长度（焊接误差不计）,试求随机变量
的分布列及
；
（2）设的取值从小到大依次为
数列
是首项为1，公差为
的等差数列，设
，当
时，求的值。
（理）（本小题满分12分）
口袋里装有大小相同的4个红球和8个白球，甲、乙两人依规则从袋中有放回摸球，每次摸出一个球，规则如下：若一方摸出一个红球，则此人继续下一次摸球；若一方摸出一个白球，则由对方接替下一次摸球，且每次摸球彼此相互独立，并由甲进行第一次摸球；求在前三次摸球中，甲摸得红球的次数ξ的分布列及数学期望.
（本小题满分12分）
一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：
（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是偶函数的概率；
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有奇函数的卡片则停止抽取，否则继续进行. 求抽取次数
的分布列、数学期望和方差.
（本小题满分12分）
2008年为山东素质教育年，为响应素质教育的实施，某中学号召学生在放假期间至少参加一次社会实践活动（以下简称活动）．现统计了该校100名学生参加活动的情况，他们参加活动的次数统计如图所示．
（1）求这些学生参加活动的人均次数；
（2）从这些学生中任选两名学生，求他们参加活动次数恰好相等的概率；
（3）从这些学生中任选两名学生，用
表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望
．
）袋中装着标有数字1，2，3的小球各2个，从袋中任取2个小球，每个小球被取出的可能性都相等．
（Ⅰ）求取出的2个小球上的数字互不相同的概率；
（Ⅱ）用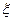
表示取出的2个小球上的数字之和，求随机变量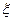的概率分布与数学期望．
（本小题满分12分）一次智力竞赛中，共分三个环节：选答、抢答、风险选答，在第一环节“选答”中．每个选手可以从6道题（其中4道选择题，2道操作题）中任意选3道题作答，答对每道题可得100分；在第二环节“抢答”中，一共为参赛选手准备了5道抢答题．答对一道得1 00分，在每一道题的抢答中，每位选手抢到的概率是相等的；在第三环节“风险选答”中，一共为选手准备了A、B、C 三类不同的题目，选手每答对一道A类、B类、C类的题目将分别得到300分、200分、100分，但如果答错，则相应地要扣除300分、200分、100分．而选手答对一道A类、B类、C类题目的概率分别是0．6、0．7、0．8，现有甲、乙、丙三位选手参加比赛，试求：（1）乙选手在第一环节中，至少选中一道操作题的概率；
（2）甲选手在第二环节中抢到的题数多于乙选手而不多于丙选手的概率；（3）在第三环节中，就每道题而言，丙选手选择哪类题目得分的期望值更大．
某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：
（Ⅰ）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
（Ⅱ）已知每吨该商品的销售利润为2千元，
表示该种商品两周销售利润的和(单位：千元).若以上述频率作为概率，且各周的销售量相互独立，求
的分布列和数学期望．
一个袋中有大小相同的标有1，2，3，4，5，6的6个小球，某人做如下游戏，每次从
袋中拿一个球（拿后放回），记下标号．若拿出球的标号是3的倍数，则得1分，否则得
分．（Ⅰ）求拿4次至少得2分的概率； （Ⅱ）求拿4次所得分数
的分布列和数学期望．
(本大题共14分)一袋中装有分别标记着1，2，3，4数字的4只小球，每次从袋中取出一只球，设每只小球被取到的可能性相同.(1)若每次取出的球不放回袋中，求恰好第三次取到标号为3的球的概率；(2)若每次取出的球放回袋中，然后再取出一只球，现连续取三次球，若三次取出的球中标号最大的数字为
，求的概率分布列与期望.
某果园要将一批水果用汽车从所在城市甲运至销售商所在城市乙。已知从城市甲到城市乙只有两条公路，且运费由果园承担。若果园恰能在约定日期（×月×日）将水果送到，则销售商一次性支付给果园20万元；若在约定日期前送到，每提前一天销售商将多支付给果园1万元。若在约定日期后运到，每迟到一天销售商将少支付给果园l万元。为保证水果新鲜度，汽车只能在约定日期的前两天出发，且只能选择其中的一条公路运送水果。已知下表内的信息：
| 统计信息 汽车行驶路线 |
不堵车的情况下到达 城市乙所需时间（天） |
堵车的情况下到达 城市乙所需时间（天） |
堵车的 概率 |
运费 （万元） |
| 公路1 |
2 |
3 |
 |
1.6 |
| 公路2 |
1 |
4 |
 |
0.8 |
（1）记汽车走公路1时果园获得的毛利润为
（单位：万元），求的分布列和数学期望
；
（2）假设你是果园的决策者，你选择哪条公路运送水果有可能让果园获得的毛利润更多?
|
注：毛利润=销售商支付给果园的费用－运费
（必做题）设
和
分别是先后抛掷一枚骰子得到的点数，用随机变量
表示方程
实根的个数（重根按一个计）．（1）求方程有实根的概率；（2）求的分布列和数学期望；
（3）求在先后两次出现的点数中有5的条件下，方程有实根的概率．
有关部门要了解甲型H1N1流感预防知识在学校的普及情况，命制了一份有10道题的问卷到各学校做问卷调查．某中学A，B两个班各被随机抽取5名学生接受问卷调查，A班5名学生得分为：5、8、9、9、9；B班5名学生得分为：6，7，8，9，10．
（1）请你估计A，B两个班中哪个班的问卷得分要稳定一些；
（2）如果把B班5名学生的得分看成一个总体，并用简单随机抽样方法从中抽取样本容量为2的样本，求样本平均数与总体平均数之差的绝对值不小于1的概率．
粤公网安备 44130202000953号
的分布列为
表示经销一件该商品的利润．（1）求事件
：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率
；（2）求
．