一个袋中有大小相同的标有1，2，3，4，5，6的6个小球，某人做如下游戏，每次从
袋中拿一个球（拿后放回），记下标号．若拿出球的标号是3的倍数，则得1分，否则得
分．（Ⅰ）求拿4次至少得2分的概率； （Ⅱ）求拿4次所得分数
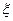的分布列和数学期望．
相关试题
中，
是
的中点，
平面
；
平面
（4分 ）
的定义域和值域.
是定义在
上的函数，
，且
，总有
恒成立．
是奇函数；
，有
，
，求：
及
；
的最小值．
的最大值，及当取最大值时x的取值集合。
的最大值.
的前 
项 和为 
已知 
，证明 数 列 
是等比数列相关知识点
推荐套卷
一个袋中有大小相同的标有1，2，3，4，5，6的6个小球，某人做如下游戏，每次从
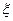袋中拿一个球（拿后放回），记下标号．若拿出球的标号是3的倍数，则得1分，否则得分．（Ⅰ）求拿4次至少得2分的概率； （Ⅱ）求拿4次所得分数的分布列和数学期望．
粤公网安备 44130202000953号