（本小题满分13分）某学习兴趣小组开展“学生语文成绩与英语成绩的关系”的课题研究，对该校高二年级800名学生上学期期末语文和英语成绩进行统计，按优秀和不优秀进行分类．记集合A={语文成绩优秀的学生}，B={英语成绩优秀的学生}．如果用
表示有限集合M中元素的个数．已知
,
,
,其中U表示800名学生组成的全集．
（1）是否有99．9%的把握认为“该校学生的语文成绩与英语成绩优秀与否有关系” ；
（2）将上述调查所得的频率视为概率，从该校高二年级的学生成绩中，有放回地随机抽取3次，记所抽取的成绩中，语文英语两科成绩中至少有一科优秀的人数为
，求的分布列和数学期望．
附：
参考数据：
 |
0．025 |
0．010 |
0．005 |
0．001 |
 |
5．024 |
6．635 |
7．879 |
10．828 |
（本小题满分12分）甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2，3，4，乙袋中红色、黑色、白色小球的个数均为3，某人用左右手分别从甲、乙两袋中取球.
（Ⅰ）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（Ⅱ）若左右手依次各取两球，称同一手中 两球颜色相同的取法为成功取法，记两次取球（左右手依次各取两球为两次取球）的成功取法次数为随机变量X，求X的分布列和数学期望.
（本小题满分13分）甲、乙两支篮球队赛季总决赛采用7场4胜制，每场必须分出胜负，场与场之间互不影响，只要有一队获胜4场就结束比赛．现已比赛了4场，且甲篮球队胜3场．已知甲球队第5，6场获胜的概率均为
，但由于体力原因，第7场获胜的概率为
．
（1）求甲队分别以
，
获胜的概率；
（2）设X表示决出冠军时比赛的场数，求X的分布列及数学期望．
（ 本小题满分12分） 某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动，要求每位同学至少参加一次活动．该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示
（1）从该班中任意选两名学生，求他们参加活动次数不相等的概率．
（2）从该班中任意选两名学生，用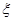
表示这两人参加活动次数之差的绝对值，求随机变量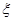的分布列及数学期望
．
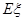（3）从该班中任意选两名学生，用
表示这两人参加活动次数之和，记“函数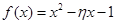
在区间（3，5）上有且只有一个零点”为事件A，求事件A发生的概率．
（本小题满分12分）口袋中装有除颜色，编号不同外，其余完全相同的2个红球，4个黑球，现从中同时取出3个球．
（1）求恰有两个黑球的概率；
（2）记取出红球的个数为随机变量
，求的分布列和数学期望
．
（本小题满分12分）甲、乙两人对弈棋局，甲胜、乙胜、和棋的概率都是
，规定有一方累计2胜或者累计2和时，棋局结束。棋局结束时，若是累计两和的情形，则宣布甲乙都获得冠军；若一方累计2胜，则宣布该方获得冠军，另一方获得亚军。设结束时对弈的总局数为X．
（1）设事件A：“X=3且甲获得冠军”，求A的概率；
（2）求X的分布列和数学期望。
某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．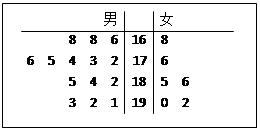
（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，再从这8人中选3人，那么至少有一人是甲部门人选的概率是多少？
（2）若从所有甲部门人选中随机选3人，用X表示所选人员中能担任助理工作的人数，写出X的分布列，并求出X的数学期望．
(本小题满分12分)
为了普及环保知识，增强环保意识，某校从理科甲班抽取60人，从文科乙班抽取50人参加环保知识测试.
（Ⅰ）根据题目条件完成下面2×2列联表，并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.
| 优秀人数 |
非优秀人数 |
总计 |
|
| 甲班 |
|||
| 乙班 |
30 |
||
| 总计 |
60 |
（Ⅱ）现已知
三人获得优秀的概率分别为
，设随机变量
表示三人中获得优秀的人数，求的分布列及期望
.附:
，
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
（Ⅰ）设
为事件"选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会"求事件
发生的概率；
（Ⅱ）设
为选出的4人中种子选手的人数，求随机变量
的分布列和数学期望.
（本小题满分12分）一汽车4S店新进A,B,C三类轿车,每类轿车的数量如下表:
| 类别 |
A |
B |
C |
| 数量 |
4 |
3 |
2 |
同一类轿车完全相同，现准备提取一部分车去参加车展.
（Ⅰ）从店中一次随机提取2辆车，求提取的两辆车为同一类型车的概率;
（Ⅱ）若一次性提取4辆车，其中A,B,C三种型号的车辆数分别记为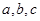
，记
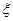为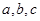的最大值，求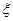的分布列和数学期望.
心理学家分析发现视觉和空间能力与性别有关， 某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学 （男30女20）， 给所有同学几何题和代数题各一题， 让各位同学自由选择一道题进行解答.选题情况如下表：（单位： 人）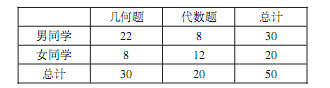
（Ⅰ）能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？
（Ⅱ）经过多次测试后， 甲每次解答一道几何题所用的时间在5—7分钟， 乙每次解答一道几何题所用的时间在6—8分钟， 现甲、 乙各解同一道几何题， 求乙比甲先解答完的概率．
（Ⅲ）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、 乙两女生被抽到的人数为X， 求X的分布列及数学期望E （X）．
附表及公式
（本小题满分12分）
某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(Ⅰ)从统计数据看，甲乙两个班哪个班成绩更稳定（用数据说明）？
(Ⅱ) 若把上表数据作为学生投篮命中率，规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作
和
，试求和的分布列和数学期望.
（本小题满分13分）在一次抽奖活动中，有甲、乙等7人获得抽奖的机会。抽奖规则如下：主办方先从7人中随机抽取两人均获奖1000元，再从余下的5人中随机抽取1人获奖600元，最后还从这5人中随机抽取1人获奖400元。
（Ⅰ）求甲和乙都不获奖的概率；
（Ⅱ）设X是甲获奖的金额，求X的分布列和均值
。
（本小题满分12分）某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神，落实“生命—和谐”教育理念和阳光体育行动的现代健康理念，学校特组织“踢毽球”大赛，某班为了选出一人参加比赛，对班上甲乙两位同学进行了
次测试，且每次测试之间是相互独立．成绩如下：（单位：个/分钟）
| 甲 |
80 |
81 |
93 |
72 |
88 |
75 |
83 |
84 |
| 乙 |
82 |
93 |
70 |
84 |
77 |
87 |
78 |
85 |
（1）用茎叶图表示这两组数据
（2）从统计学的角度考虑，你认为选派那位学生参加比赛合适，请说明理由？
（3）若将频率视为概率，对甲同学在今后的三次比赛成绩进行预测，记这三次成绩高于
个/分钟的次数为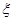
，求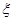的分布列及数学期望
．
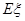（参考数据：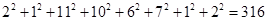
，
）
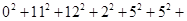
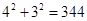粤公网安备 44130202000953号