某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人,再从这8人中选3人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选3人,用X表示所选人员中能担任助理工作的人数,写出X的分布列,并求出X的数学期望.
相关知识点
推荐套卷
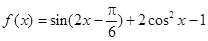
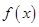 的单调增区间
的单调增区间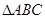 中,
中,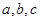 分别是角
分别是角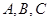 的对边,且
的对边,且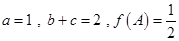 ,求
,求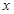 轴上,长轴长是短轴
轴上,长轴长是短轴 . 平行于OM的直线
. 平行于OM的直线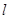 在
在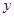 轴上的截距为
轴上的截距为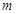
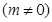 并交椭
并交椭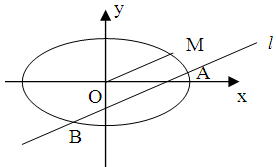
 ,动点N在圆
,动点N在圆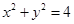 上运动,线段MN的
上运动,线段MN的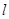 与点P的轨迹相切,且
与点P的轨迹相切,且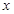 轴.
轴.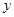 轴上的截距相等,求直线
轴上的截距相等,求直线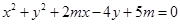 表示一个圆,
表示一个圆, 的取值范围;
的取值范围; 相交,求直线
相交,求直线 的倾斜角的取值范围.
的倾斜角的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号