（本小题满分12分）甲、乙两人对弈棋局，甲胜、乙胜、和棋的概率都是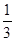
，规定有一方累计2胜或者累计2和时，棋局结束。棋局结束时，若是累计两和的情形，则宣布甲乙都获得冠军；若一方累计2胜，则宣布该方获得冠军，另一方获得亚军。设结束时对弈的总局数为X．
（1）设事件A：“X=3且甲获得冠军”，求A的概率；
（2）求X的分布列和数学期望。
中，
平面
，
，
，
，你能判定
以及
吗？
中，
，
分别是
，
的中点．
．
中，指出
，
所在直线与各个面的关系．
，
平面
，且
，
，
．
，
于
，
于
，
交
于
．（1）求证：
；（2）求证：
平面
．
相关知识点
推荐套卷
（本小题满分12分）甲、乙两人对弈棋局，甲胜、乙胜、和棋的概率都是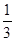，规定有一方累计2胜或者累计2和时，棋局结束。棋局结束时，若是累计两和的情形，则宣布甲乙都获得冠军；若一方累计2胜，则宣布该方获得冠军，另一方获得亚军。设结束时对弈的总局数为X．
（1）设事件A：“X=3且甲获得冠军”，求A的概率；
（2）求X的分布列和数学期望。
粤公网安备 44130202000953号